【题目】如图1，在Rt△ABC中，∠C=90°，BC=8厘米，点D在AC上，CD=3厘米．点P、Q分别由A，C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒（0＜x＜8），△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．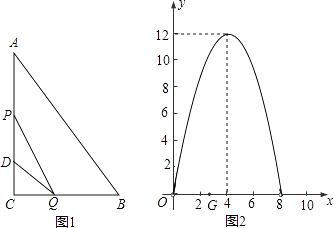

（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求点P的速度及AC的长；
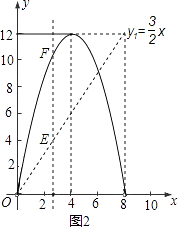
（3）在图2中，点G是x轴正半轴上一点0＜OG＜6，过G作EF垂直于x轴，分别交y1、y2的图象于点E、F．
①说出线段EF的长在图1中所表示的实际意义；
②当0＜x＜6时，求线段EF长的最大值．

参考答案：

【答案】
（1）解：∵S△DCQ= CQCD，CD=3，CQ=x，

∴y1= x（0＜x＜8）．图象如图所示；


（2）解：S△PCQ= CQCP，CP=8k﹣xk，CQ=x，

∴y2= ×（8k﹣kx）x=﹣ kx2+4kx．

∵抛物线顶点坐标是（4，12），

∴﹣ k42+4k4=12．

解得k= ．

则点P的速度每秒 厘米，AC=12厘米


（3）解：①观察图象，知线段的长EF=y2﹣y1，表示△PCQ与△DCQ的面积差（或△PDQ面积）

②由（2）得y2=﹣ x2+6x．

∴EF=﹣ x2+6x﹣ x=﹣ x2+ x=﹣ （x2﹣6x+9）+ =﹣ （x﹣3）2+ ，

∵二次项系数小于0，

∴在0＜x＜6范围，

当x=3时，EF= 最大


【解析】（1）已知了CD=3，根据Q点的速度可以用事件x表示出来CQ的长度，可根据三角形的面积计算公式得出y1与x的函数关系；（2）可先求出y2的函数解析式然后根据其顶点坐标来确定K的取值，已知了P点走完AC用时8s，因此AC=8K,而AP=kx，CQ=x，那么可根据三角形的面积公式列出关于y2与x的函数关系式，进而可根据顶点坐标求出K的值；（3）EF其实是y2-y1，也就是△PCQ与△DCQ的面积差即△PDQ面积，得出EF的函数关系式，根据自变量的取值以及函数的性质即可求出EF的最大值。

关闭