【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
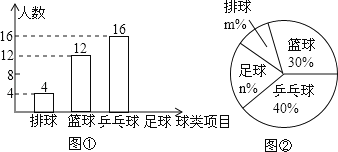
(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
参考答案:
【答案】(1)40;(2)10;20;72;(3) ![]() .
.
【解析】
试题分析:(1)根据喜欢篮球的人数与所占的百分比列式计算即可求出学生的总人数,再求出喜欢足球的人数,然后补全统计图即可;
(2)分别求出喜欢排球、喜欢足球的百分比即可得到m、n的值,用喜欢足球的人数所占的百分比乘以360°即可;
(3)画出树状图,然后根据概率公式列式计算即可得解.
试题解析:(1)九(1)班的学生人数为:12÷30%=40(人),
喜欢足球的人数为:40-4-12-16=40-32=8(人),
补全统计图如图所示;

(2)∵![]() ×100%=10%,
×100%=10%,
![]() ×100%=20%,
×100%=20%,
∴m=10,n=20,
表示“足球”的扇形的圆心角是20%×360°=72°;
(3)根据题意画出树状图如下:

一共有12种情况,恰好是1男1女的情况有6种,
∴P(恰好是1男1女)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AC=2,
 , 求菱形ABCD的面积.
, 求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是一个长为2m、宽为2n的长方形,沿图中虚线剪成四个完全一样的小长方形,然后按图2的形状拼成一个正方形.
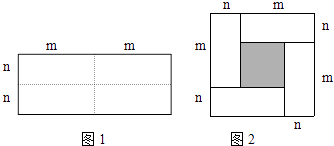
(1)图2中阴影部分的面积为;
(2)用两种不同的方法计算图2中阴影部分的面积,可以得到的等式是(只填序号); ①(m+n)2=m2+2mn+n2 ②(m﹣n)2=m2﹣2mn+n2③(m﹣n)2=(m+n)2﹣4mn
(3)若x﹣y=﹣4,xy= ,则x+y= .
,则x+y= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
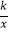 的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 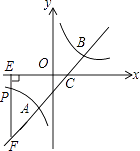
(1)反比例函数的解析式为 , 直线y=x﹣1在双曲线y=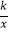 上方时x的取值范围是;
上方时x的取值范围是;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是方程x2+2x﹣2018=0的两个实数根,则a2+3a+b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2-3x的值为4,则-3x2+9x-5的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的和为10,其中一个数为x,那么表示这两个数的积的代数式是( )
A. 10x B. x(10+x) C. x(10-x) D. x(x-10)
相关试题

