【题目】如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不近似计算).

参考答案:
【答案】6![]()
【解析】试题分析:过S作AB的垂线,设垂足为C.根据三角形外角的性质,易证SB=AB.在Rt△BSC中,运用正弦函数求出SC的长.
解:过S作SC⊥AB于C.
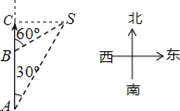
∵∠SBC=60°,∠A=30°,
∴∠BSA=∠SBC﹣∠A=30°,
即∠BSA=∠A=30°.
∴SB=AB=12.
Rt△BCS中,BS=12,∠SBC=60°,
∴SC=SBsin60°=12×![]() =6
=6![]() (海里).
(海里).
即船继续沿正北方向航行过程中距灯塔S的最近距离是6![]() 海里.
海里.
故答案为:6![]() .
.
-
科目: 来源: 题型:
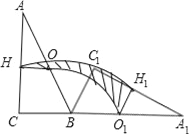
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③-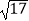 是17的平方根;
是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
A.0个
B.1
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形,它的内角和比外角和还多 180°,求这个多边形的边数.
-
科目: 来源: 题型:
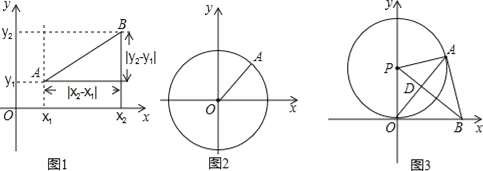
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB=
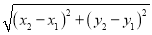 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明:AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x、y为正整数,且2x2y=32,则x、y的值共有_______对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的()
A. 三边中垂线的交点 B. 三边中线的交点
C. 三条角平分线的交点 D. 三边上高的交点
相关试题

