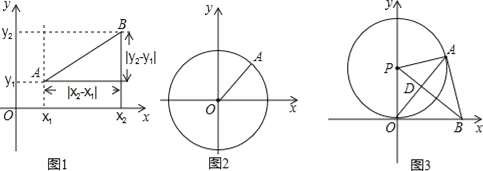
【题目】如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB=![]() 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xoy中,A(x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.
问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明:AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.
参考答案:
【答案】(x﹣a)2+(y﹣b)2=r2;①证明见解析;②存在,Q(3![]() ,3),(x﹣3
,3),(x﹣3![]() )2+(y﹣3)2=36.
)2+(y﹣3)2=36.
【解析】试题分析:问题拓展:直接根据圆的定义即可得出结论;
综合应用:①先判断出△POB≌△PAB,即可得出结论;
②先得出点Q是BP中点,再根据含30°角的直角三角形的性质确定出点B的坐标,进而得出点Q的坐标,
解:问题拓展:根据圆的定义得,(x﹣a)2+(y﹣b)2=r2,
故答案为:(x﹣a)2+(y﹣b)2=r2,
综合应用:①∵PO=PA PD⊥OA,
∴∠OPD=∠APD,
在△POB和△PAB中 ,
,
∴△POB≌△PAB,
∴∠PAB=∠POB=90°,
∴PA⊥AB
∴AB是⊙P的切线,
②存在到四点O,P,A,B距离都相等的点Q,
当点Q在线段BP中点时
∵∠POB=∠PAB=90°,
∴QO=QP=QA=QB
∴此时点Q到四点O,P,A,B距离都相等
∵PB⊥OA,∠POB=90°,∠POA=30°
∴∠PBO=30°.
∴在Rt△POB中,OP=6,
∴OB=![]() OP=6
OP=6![]() ,PB=2PO=12
,PB=2PO=12
∴B点坐标为(6![]() ,0),
,0),
∵Q是PB中点,P(0,6),B(6![]() ,0),
,0),
∴Q点坐标为(3![]() ,3)
,3)
∴OQ=![]() PB=6
PB=6
∴以Q为圆心,OQ为半径的⊙Q的方程为(x﹣3![]() )2+(y﹣3)2=36.
)2+(y﹣3)2=36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③-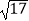 是17的平方根;
是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
A.0个
B.1
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形,它的内角和比外角和还多 180°,求这个多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不近似计算).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x、y为正整数,且2x2y=32,则x、y的值共有_______对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的()
A. 三边中垂线的交点 B. 三边中线的交点
C. 三条角平分线的交点 D. 三边上高的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )
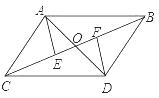
A.5对
B.6对
C.7对
D.8对
相关试题

