【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为_________.

参考答案:
【答案】4
【解析】
利用平行四边形的性质得出AD∥BC,进而得出∠AEB=∠CBF,再利用角平分线的性质得出∠ABF=∠CBF,进而得出∠AEB=∠ABF,即可得出AB=AE,同理可得:BC=CF,即可得出答案.
∵平行四边形ABCD,
∴AD∥BC,
∴∠AEB=∠CBF,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠AEB=∠ABF,
∴AB=AE,
同理可得:BC=CF,
∵AB=3cm,BC=5cm,
∴AE=3cm.CF=5cm,
∴DE=5-3=2cm,DF=5-3=2cm,
∴DE+DF=2+2=4cm,
故答案为:4cm.
-
科目: 来源: 题型:
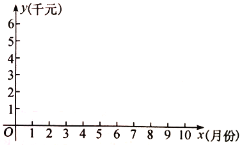
查看答案和解析>>【题目】在“美丽沧州,清洁乡村”活动中,高家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费用和每月垃圾处理费用共为
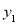 元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为
元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为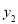 元,交费时间为x个月.
元,交费时间为x个月.(1)直接写出
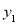 、
、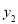 与x的函数关系式;
与x的函数关系式;(2)在同一坐标系内,画出两个函数的图像;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
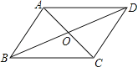
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④
 其中,正确的 是( )
其中,正确的 是( )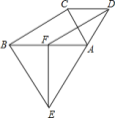
A.只有①②B.只有①②③C.只有③④D.①②③④
-
科目: 来源: 题型:
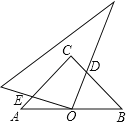
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知顶点为A的抛物线y=a(x-
 )2-2经过点B(-
)2-2经过点B(- ,2),点C(
,2),点C( ,2).
,2).(1)求抛物线的表达式;
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A-B-C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN′,若点N′落在x轴上,请直接写出Q点的坐标.

-
科目: 来源: 题型:
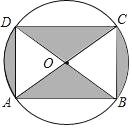
查看答案和解析>>【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
相关试题

