【题目】已知顶点为A的抛物线y=a(x-![]() )2-2经过点B(-
)2-2经过点B(-![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的表达式;
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A-B-C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN′,若点N′落在x轴上,请直接写出Q点的坐标.

参考答案:
【答案】(1) y=(x-![]() )2-2;(2)△POE的面积为
)2-2;(2)△POE的面积为![]() 或
或![]() ;(3)点Q的坐标为(-
;(3)点Q的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,2)或(
,2)或(![]() ,2).
,2).
【解析】
(1)将点B坐标代入解析式求得a的值即可得;
(2)由∠OPM=∠MAF知OP∥AF,据此证△OPE∽△FAE得![]() =
=![]()
=![]() =
=![]() ,即OP=
,即OP=![]() FA,设点P(t,-2t-1),列出关于t的方程解之可得;
FA,设点P(t,-2t-1),列出关于t的方程解之可得;
(3)分点Q在AB上运动、点Q在BC上运动且Q在y轴左侧、点Q在BC上运动且点Q在y轴右侧这三种情况分类讨论即可得.
(1)把点B(-![]() ,2)代入y=a(x-
,2)代入y=a(x-![]() )2-2,
)2-2,
解得a=1,
∴抛物线的表达式为y=(x-![]() )2-2,
)2-2,
(2)由y=(x-![]() )2-2知A(
)2-2知A(![]() ,-2),
,-2),
设直线AB表达式为y=kx+b,代入点A,B的坐标得 ,
,
解得![]() ,
,
∴直线AB的表达式为y=-2x-1,
易求E(0,-1),F(0,-![]() ),M(-
),M(-![]() ,0),
,0),
若∠OPM=∠MAF,
∴OP∥AF,
∴△OPE∽△FAE,
∴![]() ,
,
∴OP=![]() FA=
FA=![]()
![]() ,
,
设点P(t,-2t-1),则![]() ,
,
解得t1=-![]() ,t2=-
,t2=-![]() ,
,
由对称性知,当t1=-![]() 时,也满足∠OPM=∠MAF,
时,也满足∠OPM=∠MAF,
∴t1=-![]() ,t2=-
,t2=-![]() 都满足条件,
都满足条件,
∵△POE的面积=![]() OE·|t|,
OE·|t|,
∴△POE的面积为![]() 或
或![]() ;
;
(3)如图,若点Q在AB上运动,过N′作直线RS∥y轴,交QR于点R,交NE的延长线于点S,

设Q(a,-2a-1),则NE=-a,QN=-2a.
由翻折知QN′=QN=-2a,N′E=NE=-a,
由∠QN′E=∠N=90°易知△QRN′∽△N′SE,
∴![]() =
=![]() =
=![]() ,即
,即![]() ==
==![]() =2,
=2,
∴QR=2,ES=![]() ,
,
由NE+ES=NS=QR可得-a+![]() =2,
=2,
解得a=-![]() ,
,
∴Q(-![]() ,
,![]() ),
),
如图,若点Q在BC上运动,且Q在y轴左侧,过N′作直线RS∥y轴,交BC于点R,交NE的延长线于点S.

设NE=a,则N′E=a.
易知RN′=2,SN′=1,QN′=QN=3,
∴QR=![]() ,SE=
,SE=![]() -a.
-a.
在Rt△SEN′中,(![]() -a)2+12=a2,
-a)2+12=a2,
解得a=![]() ,
,
∴Q(-![]() ,2),
,2),
如图,若点Q在BC上运动,且点Q在y轴右侧,过N′作直线RS∥y轴,交BC于点R,交NE的延长线于点S.

设NE=a,则N′E=a.
易知RN′=2,SN′=1,QN′=QN=3,
∴QR=![]() ,SE=
,SE=![]() -a.
-a.
在Rt△SEN′中,(![]() -a)2+12=a2,
-a)2+12=a2,
解得a=![]() ,
,
∴Q(![]() ,2).
,2).
综上,点Q的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,2)或(
,2)或(![]() ,2).
,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边三角形△ACD和△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④
 其中,正确的 是( )
其中,正确的 是( )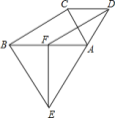
A.只有①②B.只有①②③C.只有③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
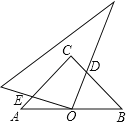
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
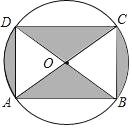
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.
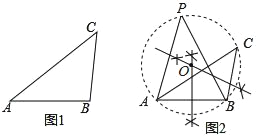
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

相关试题

