搜索
【题目】如图，在长方形 ABCD 中，放入六个形状大小相同的长方形，所标尺寸如图所示， 则图中阴影部分面积为（ ）
A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
参考答案：
【答案】A
【解析】
本题通过图像发现小长方形和大长方形的长和宽的联系从而列式，设长方形的长和宽为未知数，根据图示可得到关于x，y的两个方程，可求得解，从而可得到大长方形的面积，再根据阴影部分的面积=大长方形的面积-6个小长方形的面积求解即可.
设小长方形的长为x，宽为y，如图可知，
x+3y=14，①
x+y-2y=6，即x-y=6，②
①-②得4y=8，y=2，
代入②得x=8，
因此，大矩形ABCD的宽AD=6+2y=6+2×2=10．
矩形ABCD面积=14×10=140（平方厘米），
阴影部分总面积=140-6×2×8=44（平方厘米）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】找规律
如图①所示的是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间的小三角形三边的中点，得到图③，按此方法继续连接，请你根据每个图中三角形的个数的规律完成各题。
（1）将下表填写完整；
图形编号
①
②
③
④
⑤
…
三角形个数
1
5
…
（2）在第n个图形中有_________________个三角形。(用含n的式子表示)
（3）按照上述方法，能否得到2019个三角形?如果能，请求出n；如果不能，请简述理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，点D是BC边上一点，以AD为直径的⊙O与BC相切于点D，与AD、AC分别交于点E、F．
（1）如图①，若∠AEF=52°，求∠C的度数．
（2）如图②，若EF经过点O，且∠AEF=35°，求∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A、B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：
种植户
种植A类蔬菜面积
（单位：亩）
种植B类蔬菜面积
（单位：亩）
总收入
（单位：元）
甲
3
1
12500
乙
2
3
16500
说明：不同种植户种植的同类蔬菜每亩平均收入相等．
（1）求A、B两类蔬菜每亩平均收入各是多少元？
（2）某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需要绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长（结果保留整数）
（参考数据：sin67°≈0.92；cos67°≈0.38；
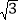≈1.73）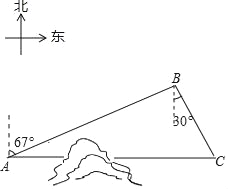
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+1经过A(-1，0)，B(1，1)两点．
(1)求该抛物线的解析式；
(2)阅读理解：
在同一平面直角坐标系中，直线l1：y=k1x+b1(k1，b1为常数，且k1≠0)，直线l2：y=k2x+b2(k2，b2为常数，且k2≠0)，若l1⊥l2，则k1·k2=-1．
解决问题：
①若直线y=3x-1与直线y=mx+2互相垂直，求m的值；
②是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；
(3)M是抛物线上一动点，且在直线AB的上方(不与A，B重合)，求点M到直线AB的距离的最大值．
相关试题
