【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
参考答案:
【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1) 根据题意画出树状图即可.
(2)分别将各点坐标代入函数y=-x2-1解析式, 若等式成立, 则该点在其图象上, 用满足条件的M点的个数除以M点总个数即为所求概率。
(3) 分别计算各点到0点的距离, 若OM> 2, 则在⊙0上或⊙0外, 可以过M点作⊙0的切线,满足条件的M点的个数除以M点总个数即为所求概率.
解:(1) 树状图如图所示, 则M所有可能的坐标有9种情况,分别为:(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0).
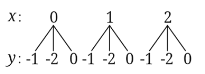
(2) 将 (1) 中的9个坐标分别代入函数y=-x2-1, 可得在函数的图象上的M点有两个: (0,-1), (1,-2),所以点M在函数y=-x2+1的图象上的概率为![]() .
.
(3) 要过M作圆的切线, 则该点应该在圆上或者圆外, 通过比较OM与半径长度可知, 点M在⊙0上或⊙0外的有5个, 分别为(0,-2),(1,-2),(2,-1),(2,-2),(2,0).则过M点能作⊙0的切线的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
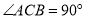 ,
,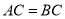 ,
,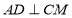 ,
,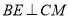 ,垂足分别为
,垂足分别为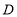 ,
,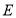 ,
,(1)如图1,①线段
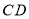 和
和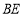 的数量关系是__________;
的数量关系是__________;②请写出线段
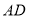 ,
,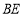 ,
,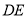 之间的数量关系并证明.
之间的数量关系并证明.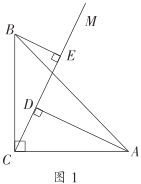
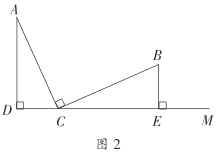
(2)如图2,若已知条件不变,上述结论②还成立吗?如果不成立,请直接写出线段
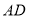 ,
,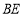 ,
, 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明解方程
 =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )
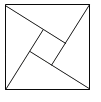
A.2B.0.5C.13D.1
-
科目: 来源: 题型:
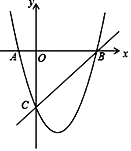
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
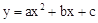 (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论:
(1)二次函数
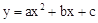 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;(2)当
 时,y<0;
时,y<0;(3)二次函数
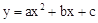 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
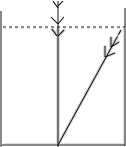
查看答案和解析>>【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.
相关试题

