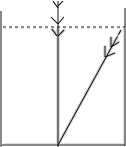
【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.
参考答案:
【答案】x2+52=(x+1)2.
【解析】
我们可以将其转化为数学几何图形,如图所示,根据题意,可知EB'的长为10尺,则B'C=5尺,设出AB=AB'=x尺,表示出水深AC,根据勾股定理建立方程即可.
依题意画出图形,
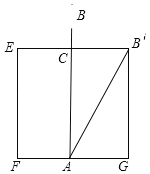
设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,因为B'E=10尺,所以B'C=5尺,
在Rt△AB'C中,∵CB′2+AC2=AB′2
∴52+(x﹣1)2=x2,
故答案为:x2+52=(x+1)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
-
科目: 来源: 题型:
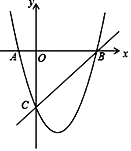
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
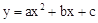 (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论:
(1)二次函数
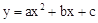 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;(2)当
 时,y<0;
时,y<0;(3)二次函数
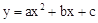 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

-
科目: 来源: 题型:
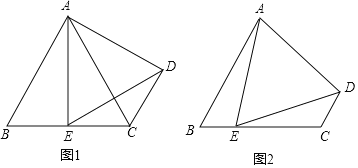
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象的对称轴是直线
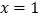 ,它与
,它与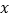 轴交于
轴交于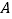 、
、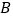 两点,与
两点,与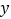 轴交与点
轴交与点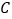 ,点
,点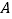 、
、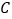 的坐标分别是
的坐标分别是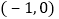 、
、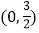 .
.
(1)请在平面直角坐标系内画出示意图;
(2)求此图象所对应的函数关系式;
(3)若点
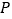 是此二次函数图象上位于
是此二次函数图象上位于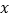 轴上方的一个动点,求
轴上方的一个动点,求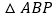 面积的最大值.
面积的最大值.
相关试题

