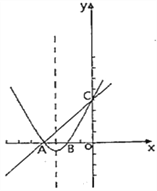
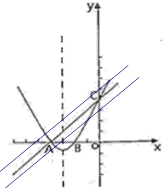
【题目】在平面直角坐标系xoy中,抛物线y=ax2+bx+c (a≠O)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(-4,O),抛物线的对称轴是直线x=-3,且经过A、C两点的直线为y=kx+4.
(1)求抛物线的函数表达式;
(2)将直线AC向下平移m个单位长度后,得到的直线l与抛物线只有一个交点D,求m的值;
(3)抛物线上是否存在点Q,使点Q到直线AC的距离为![]() ?若存在,请直接写出Q的坐标,若不存在,请说明理由.
?若存在,请直接写出Q的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
, ![]()
![]() ,
, ![]() .
.
【解析】试题分析:(1)由经过A、C两点直线为y=kx+4,且点C在y轴上,确定出点C坐标,根据抛物线的对称性确定出B点坐标,然后用待定系数法即可求得抛物线的解析式;
(2)根据点A的坐标确定出直线AC的解析式,根据平移设平移后的解析式为y=x+4-m ,与![]() 联立组成方程组,根据只有一个交点,利用根据的判别式即可求得m的值;
联立组成方程组,根据只有一个交点,利用根据的判别式即可求得m的值;
(3)由AC:y=x+4可知到直线AC距离为![]() 的点在直线y=x+3或直线y=x+5上,分情况进行讨论即可得.
的点在直线y=x+3或直线y=x+5上,分情况进行讨论即可得.
试题解析:(1)∵经过![]() 、
、![]() 两点直线为
两点直线为![]() ,且点
,且点![]() 在
在![]() 轴上,
轴上,
∴C(0,4),
∵抛物线的对称轴是直线![]() ,A(-4,0),
,A(-4,0),
∴B(-2,0),
∴设抛物线的解析式为: ![]() ,
,
∵抛物线经过点![]() (0,4),
(0,4),
∴![]() ,
,
解得: ![]() ,
,
∴抛物线的函数表达式为![]() ;
;
(2)将![]() 代入
代入![]() ,
,
得 ![]() ,
,
解得![]() ,
,
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∵直线![]() 是由直线
是由直线![]() 向下平移
向下平移![]() 个单位得到的,
个单位得到的,
∴设直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 与抛物线相交,
与抛物线相交,
∴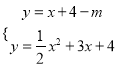 ,
,
∵只有一个交点,
∴![]() ,
,
即: ![]() ,
,
∴m=2;
(3)由AC:y=x+4可知到直线AC距离为![]() 的点在直线y=x+3或直线y=x+5上,
的点在直线y=x+3或直线y=x+5上,
解方程组 或
或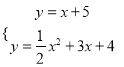 ,
,
得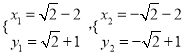 或
或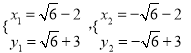 ,
,
所以Q点坐标为: ![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是8,求线段BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△
 ;
;(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△
 ;
;(3)将点B绕坐标原点逆时针方向旋转90°至点
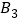 ,则点
,则点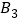 的坐标为(______,______)
的坐标为(______,______)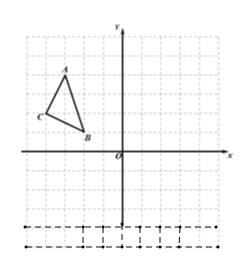
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=bx2+a的图象可能是( )
A.
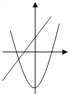 B.
B. 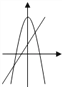 C.
C. 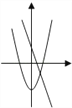 D.
D. 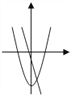
-
科目: 来源: 题型:
查看答案和解析>>【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

相关试题

