【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是8,求线段BF的长.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)过点O作OM⊥AB,垂足是M,证明OM等于圆的半径OD即可;
(2)过点O作ON⊥BE,垂足是N,连接OF,则四边形OMBN是矩形,在直角△OBM利用三角函数求得OM和BM的长,则BN和ON即可求得,在直角△ONF中利用勾股定理求得NF,则BF即可求解.
试题解析:(1)过点O作OM⊥AB,垂足是M ,
∵⊙O与AC相切于点D ,∴OD⊥AC ,∴∠ADO=∠AMO=90°,
∵△ABC是等边三角形, AO⊥BC,∴OA是∠MAD的角平分线,
∵OD⊥AC,OM⊥AB,∴OM=OD ,
∴AB与⊙O相切;
(2)过点O作ON⊥BE,垂足是N,连接OF ,
∵AB=AC,AO⊥BC ,
∴O是BC的中点,
∴![]() ,
,
在直角△ABC中,∠ABE=90°,∠MBO=60°,
∴∠OBN=30° ,
∵ON⊥BE,∠OBN=30°,OB=4,
∴![]() ,
, ![]() ,
,
∵AB⊥BE,
∴四边形OMBN是矩形,
∴![]() ,
,
∵![]() ,
,
由勾股定理得![]() ,
,
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

-
科目: 来源: 题型:
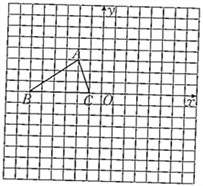
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空:以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△
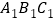 ;
;(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△
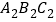 ;
;(3)将点B绕坐标原点逆时针方向旋转90°至点
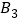 ,则点
,则点 的坐标为(______,______)
的坐标为(______,______)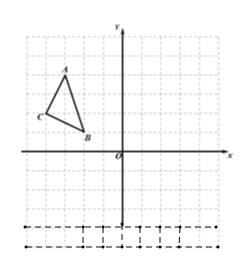
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,抛物线y=ax2+bx+c (a≠O)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(-4,O),抛物线的对称轴是直线x=-3,且经过A、C两点的直线为y=kx+4.
(1)求抛物线的函数表达式;
(2)将直线AC向下平移m个单位长度后,得到的直线l与抛物线只有一个交点D,求m的值;
(3)抛物线上是否存在点Q,使点Q到直线AC的距离为
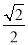 ?若存在,请直接写出Q的坐标,若不存在,请说明理由.
?若存在,请直接写出Q的坐标,若不存在,请说明理由.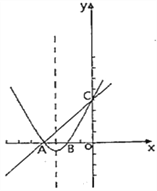
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=bx2+a的图象可能是( )
A.
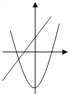 B.
B. 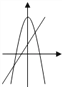 C.
C. 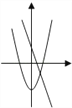 D.
D. 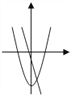
相关试题

