【题目】如图,DF∥AC,E点为DF上的点,B为AC上的点,∠1=∠2.求证:∠C=∠D.请你根据条件进行推理,得出结论,并在括号内注明原因.

证明:∵∠1=∠2(已知)
∠1=∠3,∠2=∠4(_______),
∴∠3=∠4(等量代换),
∴_____∥_____(_______),
∴∠C=∠ABD(_______),
∵DF∥AC(已知)
∴∠D=∠ABD(_______),
∴∠C=∠D(_______).
参考答案:
【答案】对顶角相等 DB EC 内错角相等,两直线平行 两直线平行,同位角相等 两直线平行,内错角相等 等量代换
【解析】
根据∠1=∠2,再根据对顶角相等可知:∠1=∠3,∠2=∠4,等到∠3=∠4,利用内错角相等,两直线平行,得到BD∥CE,根据平行线的性质,得到∠DBA=∠C,根据DF∥AC,利用平行线的性质,得到∠D=∠DBA,进而得到∠C=∠D,故得证.
证明:∵∠1=∠2(已知)
∠1=∠3,∠2=∠4(对顶角相等),
∴∠3=∠4(等量代换),
∴DB∥EC( 内错角相等,两直线平行),
∴∠C=∠ABD(两直线平行,同位角相等),
∵DF∥AC(已知)
∴∠D=∠ABD(两直线平行,内错角相等),
∴∠C=∠D(等量代换).
故答案为:对顶角相等;DB;EC;内错角相等,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程
 下列说法:①当
下列说法:①当 时,则方程
时,则方程 一定有一根为
一定有一根为 ;②若
;②若 则方程
则方程 一定有两个不相等的实数根;③若
一定有两个不相等的实数根;③若 是方程
是方程 的一个根,则一定有
的一个根,则一定有 ;④若
;④若 ,则方程
,则方程 有两个不相等的实数根。其中正确的是( )
有两个不相等的实数根。其中正确的是( )A.①②B.①③C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为-1,正方形ABCD的面积为16.
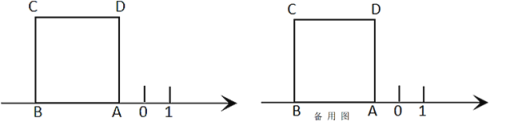
(1)数轴上点B表示的数为___;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为A′B′C′D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S.
①当S=4时,画出图形,并求出数轴上点A′表示的数;
②设正方形ABCD的移动速度为每秒2个单位长度,点E为线段AA′的中点,点F在线段BB′上,且BF=
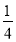 BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 -1来表示
-1来表示 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵
 ,即
,即 ,
,∴
 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( -2).
-2).请解答:(1)
 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
 的小数部分为a,
的小数部分为a,  的整数部分为b,求a+b-
的整数部分为b,求a+b- 的值;
的值;(3)已知: 10+
 =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个数值转换器,如图所示:

(1)当输入的x为16时.输出的y值是 ;
(2)若输入有效的x值后,始终输不出y值,请写出所有满足要求的x的值,并说明你的理由;
(3)若输出的y是
 ,请写出两个满足要求的x值: .
,请写出两个满足要求的x值: .
相关试题

