【题目】苏科版《数学》八年级上册第35页第2题,介绍了应用构造全等三角形的方法测量了池塘两端A、B两点的距离.星期天,爱动脑筋的小刚同学用下面的方法也能够测量出家门前池塘两端A、B两点的距离.他是这样做的:
选定一个点P,连接PA、PB,在PM上取一点C,恰好有PA=14m,PB=13m,PC=5m,BC=12m,他立即确定池塘两端A、B两点的距离为15m.
小刚同学测量的结果正确吗?为什么?

参考答案:
【答案】小刚同学测量的结果正确,理由见解析.
【解析】
由勾股定理的逆定理证出△BCP是直角三角形,∠BCP=90°,得出∠ACB=90°,再由勾股定理求出AB即可.
解:小刚同学测量的结果正确,理由如下:
∵PA=14m,PB=13m,PC=5m,BC=12m,
∴AC=PA﹣PC=9m,PC2+BC2=52+122=169,PB2=132=169,
∴PC2+BC2=PB2,
∴△BCP是直角三角形,∠BCP=90°,
∴∠ACB=90°,
∴AB=![]() =
=![]() =15(m).
=15(m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=5,AD=BC=13,点E为射线AD上的一个动点,若△ABE与△A'BE关于直线BE对称,当△A'BC为直角三角形时,AE的长为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.求证:
(1)AB∥CD;
(2)点M是线段EF的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,点E在AC的垂直平分线上.
(1)若AB=5,BC=7,求△ABE的周长;
(2)若∠B=57°,∠DAE=15°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C、D.①△OB1C∽△OA1D; ②OAOC=OBOD;③OCG=ODF1;④F=F1.
其中正确的说法有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:如图1,在△ABC中,点D是BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①BE、CF与EF之间的关系为:BE+CF EF;(填“>”、“=”或“<”)
②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
问题解决:如图2,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=130°,以D为顶点作∠EDF=65°,∠EDF的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
-
科目: 来源: 题型:
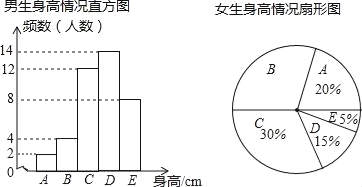
查看答案和解析>>【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表:
组别
身高(cm)
A
x<150
B
150≤x<155
C
155≤x<160
D
160≤x<165
E
x≥165
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)男生身高的中位数落在 组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有 人,身高人数最多的在 组(填组别序号);
(3)已知该校共有男生400人、女生420人,请估计身高不足160cm的学生约有多少人?
相关试题

