Question

【题目】如图，长方形ABCD中，∠A＝∠ABC＝∠BCD＝∠D＝90°，AB＝CD＝5，AD＝BC＝13，点E为射线AD上的一个动点，若△ABE与△A'BE关于直线BE对称，当△A'BC为直角三角形时，AE的长为__．

Answer 1

【答案】1或25．

【解析】

分点E在线段AD上，点E在线段AD的延长线上两种情况讨论，由题意可得AB=A'B=5，∠EA'B=90°，AE=A'E，A'C=12，根据勾股定理和全等三角形的性质，可求AE的长．

解：若点E在线段AD上，

∵若△ABE与△A′BE关于直线BE对称，

∴AB＝A'B＝，5，∠EA'B＝90°，AE＝A'E

∵△A'BC为直角三角形

∴∠BA'C＝90°

∴A'C＝＝＝12，

∵∠EA'B＝90°，∠BA'C＝90°

∴∠CA'E＝180°

∴点E，点C，点A'共线

在Rt△CDE中，DC2+DE2＝CE2．

∴（A'E+12）2＝（13﹣AE）2+25，

∴AE＝1，

若点E在线段AD的延长线上，且点C在A'E上，如图所示：

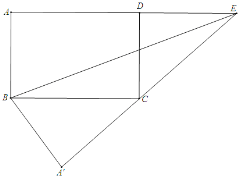
∵△ABE与△A′BE关于直线BE对称，

∴AB＝A'B＝，5，∠A＝∠A'＝90°

在Rt△A'BC中，A'C＝＝＝12，

∵∠BCA'+∠DCE＝90°，∠DCE+∠DEC＝90°

∴∠BCA'＝∠DEC，

∵∠A'＝∠EDC＝90°，AB＝CD＝A'B，

∴在△A'C和△DCE中，，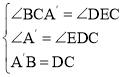

∴△A'BC≌△DCE（AAS），

∴DE＝A'C＝12，

∴AE＝1AD+DE＝13+12＝25；

故答案为：1或25．