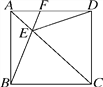
【题目】(9分)如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF; (2)BE=CF
参考答案:
【答案】证明:
(1)∵AC∥DF,
∴∠ACB=∠F,………………………………2分
在△ABC和△DEF中, ,……4分
,……4分
∴△ABC≌△DEF(AAS);………………………………………………………6分
(2)∵△ABC≌△DEF,
∴BC=EF,………………………………………………………………………8分
∴BC-CE=EF-CE,
即BE=CF.………………………………………………………………………9分
【解析】
试题证明:(1)∵AC∥DF
∴∠ACB=∠F
在△ABC与△DEF中

∴△ABC≌△DEF
(2) ∵△ABC≌△DEF
∴BC=EF
∴BC–EC=EF–EC
即BE=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=
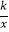 (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE. 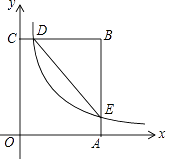
(1)连接OE,若△EOA的面积为3,则k=;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
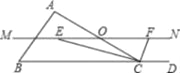
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F.
(1)求证:EO=FO;(2)若CE=4,CF=3,你还能得到那些结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.

(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )

A. 图①中点A的实际意义是公交公司运营后亏损1万元
B. 图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡
C. 图②能反映公交公司意见
D. 图③能反映乘客意见
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了支持国货,哈市某手机卖场计划用
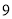 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌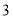 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表: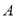 种
种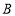 种
种 种
种进价(元/部)
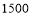
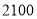
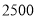
售价(元/部)
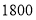
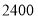
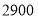
若该手机卖场同时购进两种不同型号的手机
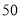 台,
台,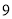 万元刚好用完.
万元刚好用完.(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润
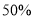 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
相关试题

