【题目】已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3).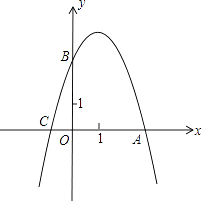
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标解:;
(3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+2x+c的图象经过点A(3,0)和点B(0,3),
∴ ![]() ,解得a=﹣1,c=3,
,解得a=﹣1,c=3,
∴抛物线的解析式为:y=﹣x2+2x+3.
(2)
对称轴为x= ![]() =1,
=1,
令y=﹣x2+2x+3=0,解得x1=3,x2=﹣1,∴C(﹣1,0).
如图1所示,连接AB,与对称轴x=1的交点即为所求之D点,由于A、C两点关于对称轴对称,则此时DB+DC=DB+DA=AB最小.
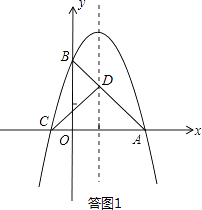
设直线AB的解析式为y=kx+b,由A(3,0)、B(0,3)可得:
![]() ,解得k=﹣1,b=3,
,解得k=﹣1,b=3,
∴直线AB解析式为y=﹣x+3.
当x=1时,y=2,∴D点坐标为(1,2).
(3)
解:结论:存在.
如图2所示,
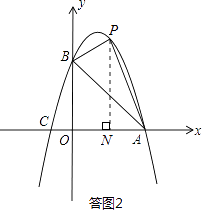
设P(x,y)是第一象限的抛物线上一点,
过点P作PN⊥x轴于点N,则ON=x,PN=y,AN=OA﹣ON=3﹣x.
S△ABP=S梯形PNOB+S△PNA﹣S△AOB
= ![]() (OB+PN)ON+
(OB+PN)ON+ ![]() PNAN﹣
PNAN﹣ ![]() OAOB
OAOB
= ![]() (3+y)x+
(3+y)x+ ![]() y(3﹣x)﹣
y(3﹣x)﹣ ![]() ×3×3
×3×3
= ![]() (x+y)﹣
(x+y)﹣ ![]() ,
,
∵P(x,y)在抛物线上,∴y=﹣x2+2x+3,代入上式得:
S△ABP= ![]() (x+y)﹣
(x+y)﹣ ![]() =﹣
=﹣ ![]() (x2﹣3x)=﹣
(x2﹣3x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,S△ABP取得最大值.
时,S△ABP取得最大值.
当x= ![]() 时,y=﹣x2+2x+3=
时,y=﹣x2+2x+3= ![]() ,∴P(
,∴P( ![]() ,
, ![]() ).
).
所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;P点的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)利用待定系数法求出抛物线的解析式;(2)连接AB,与对称轴x=1的交点即为所求之D点.为求D点坐标,需先求出直线AB的解析式,然后令x=1求得y,即可求出D点坐标;(3)本问关键是求出△ABP的面积表达式.这个表达式是一个关于P点横坐标的二次函数,利用二次函数求极值的方法可以确定P点的坐标.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:
已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4, ①
所以c2(a2-b2)=( a2-b2)( a2+b2). ②
所以c2= a2+b2. ③
所以△ABC是直角三角形. ④
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代码为 ;
(2)错误的原因为 ;
(3)请你将正确的解答过程写下来.
-
科目: 来源: 题型:
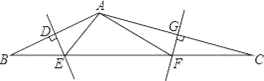
查看答案和解析>>【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx﹣k与反比例函数
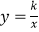 在同一直角坐标系中的大致图象是( )
在同一直角坐标系中的大致图象是( )
A.
B.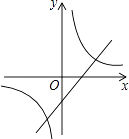
C.
D.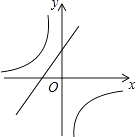
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式(mx2+2mx-1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均匀分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于________;
(2)请你用两种不同的方法表示图②中阴影部分的面积,方法一:__________________,方法二:________________;
(3)观察图②,你能写出代数式(m+n)2,(m-n)2,mn之间的关系吗?
(4)应用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
相关试题

