【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均匀分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于________;
(2)请你用两种不同的方法表示图②中阴影部分的面积,方法一:__________________,方法二:________________;
(3)观察图②,你能写出代数式(m+n)2,(m-n)2,mn之间的关系吗?
(4)应用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
参考答案:
【答案】(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn或(m+n)2=(m-n)2+4mn或4mn=(m+n)2-(m-n)2(写出一个即可);(4)m=7,n=4.
【解析】
对于(1),根据图形,利用面积将阴影部分的面积表示出来,然后根据正方形的面积计算公式计算出阴影部分的正方形的边长;
对于(2),根据图形的面积计算,进而得出表示图②中阴影部分面积的两种不同的方法;
对于(3),根据图形的面积进而得出(m+n)2,(m-n)2,mn之间的关系;
对于(4),由(3)可知(m-n)2=(m+n)2-4mn,由m+n=11、mn=28可得出m-n=3,由m+n=11进而得出m,n的值.
(1)m-n
(2)(m-n)2 (m+n)2-4mn
(3)(m-n)2=(m+n)2-4mn或(m+n)2=(m-n)2+4mn或4mn=(m+n)2-(m-n)2(写出一个即可).
(4)因为(m-n)2=(m+n)2-4mn=112-4×28=9,
所以m-n=3(m>n,负值已舍去),
所以![]() 解得
解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3).
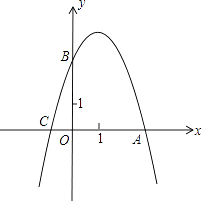
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标解:;
(3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx﹣k与反比例函数
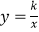 在同一直角坐标系中的大致图象是( )
在同一直角坐标系中的大致图象是( )
A.
B.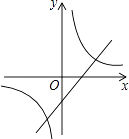
C.
D.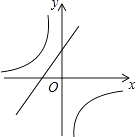
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式(mx2+2mx-1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
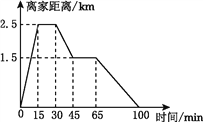
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
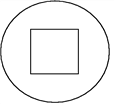
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
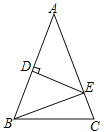
相关试题

