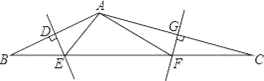
【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
参考答案:
【答案】 10 140°
【解析】(1)∵ED、FG分别是AB、AC的垂直平分线,
∴AE=BE,AF=CF,
∵△AEF的周长为10cm,
∴AC=10cm;
(2)∵∠EAF=100°,
∴∠AEF+∠AFE=80°,
∵ED、FG分别是AB、AC的垂直平分线,
∴EA=EB,FA=FC,
∴∠AEF=2∠EAB,∠AFE=2∠CAF,
∴∠BAC=∠EAF+∠EAB+∠FAC=100°+∠EAB+∠CAF=100°+12(∠AEF+∠AFE)=140°.
故答案为:10,140°.
点睛: 本题主要考查了线段的垂直平分线的性质等几何知识,线段的垂直平分线上的点到线段的两个端点的距离相等,以及外角的性质,难度适中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=(2m+2)x+4中,y随x的增大而增大,那么m的值是( )
A.0 B.-1 C.-1.5 D.-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是_________________
-
科目: 来源: 题型:
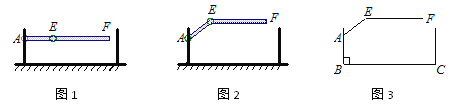
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
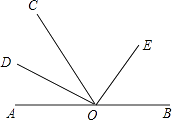
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
相关试题

