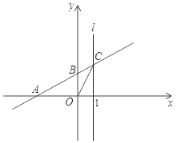
【题目】如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C,连结OC.
(1)△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.
(2)若m=2,点T在直线l上且TA=TB,求点T的坐标.
参考答案:
【答案】(1)△OBC的面积与△OAC的面积比是定值,△OBC的面积与△OAC的面积比是![]() ;(2)T(1,﹣
;(2)T(1,﹣![]() ).
).
【解析】
(1)设直线AB的解析式为y=kx+b,由A和点B得到![]() ;当x=1时,y=
;当x=1时,y=![]() ,得到C点,从而得出
,得到C点,从而得出![]() 为定值.
为定值.
(2)有已知条件得y=![]() x+2,设AB的垂直平分线的解析式为:y=﹣
x+2,设AB的垂直平分线的解析式为:y=﹣![]() x+n,由线段AB的中点坐标为(﹣1.5,1),得n=﹣
x+n,由线段AB的中点坐标为(﹣1.5,1),得n=﹣![]() ,则解析式为:y=﹣
,则解析式为:y=﹣![]() x﹣
x﹣![]() ,最后得到T的坐标.
,最后得到T的坐标.
(1)△OBC的面积与△OAC的面积比是定值,
理由:设直线AB的解析式为y=kx+b,
∵点A(﹣3,0),点B(0,m),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=![]() x+m,
x+m,
当x=1时,y=![]() ,
,
∴C(1,![]() ),
),
∴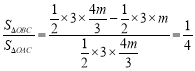 ,
,
∴△OBC的面积与△OAC的面积比是定值;
(2)∵m=2,
∴点B(0,2),
∴直线AB的解析式为y=![]() x+2,
x+2,
∵点T在直线l上且TA=TB,
∴点T在线段AB的垂直平分线上,
设AB的垂直平分线的解析式为:y=﹣![]() x+n,
x+n,
∵线段AB的中点坐标为(﹣1.5,1),
∴n=﹣![]() ,
,
∴AB的垂直平分线的解析式为:y=﹣![]() x﹣
x﹣![]() ,
,
当x=1时,y=﹣![]() ,
,
∴T(1,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表
售价x(单位:元/千克)
30
25
20
每天销售量y(单位:千克)
5
55
105
如果已知草莓每天销量y与售价x(30.5>x>14)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克,哪天的销售利润更高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,
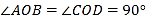 ,
,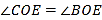 ,点
,点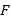 为
为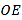 反向延长线上一点(图中所有角均指小于
反向延长线上一点(图中所有角均指小于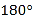 的角).下列结论:①
的角).下列结论:①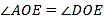 ;②
;②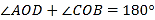 ;③
;③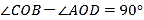 ;④
;④ .其中正.确.结论的个数有( ).
.其中正.确.结论的个数有( ).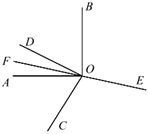
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“禁毒知识竞赛”,从中抽取了部分学生,将他们的竞赛成绩进行统计后分为
 ,
,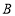 ,
,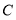 ,
,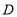 四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:
四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题: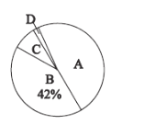
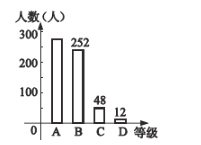
(1)抽取了_______名学生成绩;
(2)扇形统计图中
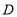 等级所在扇形的圆心角度数是_________;
等级所在扇形的圆心角度数是_________;(3)为估算全校八年级“禁毒知识竞赛”平均分,现将
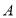 、
、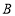 、
、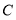 、
、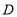 依次记作
依次记作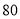 分、
分、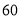 分、
分、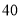 分、
分、 分,请估算该校八年级知识竞赛平均分.
分,请估算该校八年级知识竞赛平均分. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有公共端点
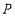 的两条线段
的两条线段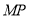 ,
,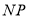 组成一条折线
组成一条折线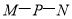 ,若该折线
,若该折线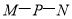 上一点
上一点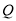 把这条折线分成相等的两部分,我们把这个点
把这条折线分成相等的两部分,我们把这个点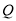 叫做这条折线的“折中点”.已知点
叫做这条折线的“折中点”.已知点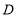 是折线
是折线 的“折中点”,点
的“折中点”,点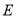 为线段
为线段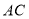 的中点,
的中点,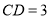 ,
,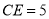 ,则线段
,则线段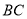 的长为______.
的长为______.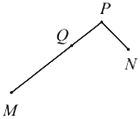
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批自行车. 男式自行车价格为
 元/辆,女式自行车价格为
元/辆,女式自行车价格为 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多 辆,设购进女式自行车
辆,设购进女式自行车 辆,购置总费用为
辆,购置总费用为 元.
元.(1)求购置总费用
 (元)与女式单车
(元)与女式单车 (辆)之间的函数关系式;
(辆)之间的函数关系式;(2)若两种自行车至少需要购置
 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮
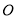 在航行过程中,发现灯塔
在航行过程中,发现灯塔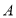 在它的南偏东
在它的南偏东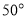 方向上.同时,在它的北偏东
方向上.同时,在它的北偏东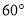 、西北(西偏北
、西北(西偏北 )方向上又分别发现了客轮
)方向上又分别发现了客轮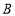 和海岛
和海岛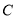 .
.
(1)仿照表示灯塔方位的方法,分别画出客轮
 和海岛
和海岛 方向的射线;
方向的射线;(2)另一货轮
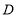 在平面内所组成的
在平面内所组成的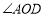 与
与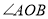 互为补角,请画出货轮
互为补角,请画出货轮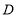 方向的射线并写出所在的方位角.
方向的射线并写出所在的方位角.
相关试题

