【题目】用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板.
(1)现需150块C型钢板、180块D型钢板,则怡好用A型、B型钢板各多少块?
(2)若A、B型钢板共100块,现需C型钢板至多150块,D型钢板不超过170块,共有几种方案?
(3)若需C型钢板80块,D型钢板不多于45块(A型、B型钢板都要使用).求A、B型钢板各需多少块?
参考答案:
【答案】(1)用A型钢板40块、B型钢板70块;(2)共21种方案;(3)A型钢板39块,B型钢板2块.
【解析】
(1)根据题意设用A型钢板x块,用B型钢板y块,再利用现需150块C型钢板、180块D型钢板分别得出等式组成方程组进而求出即可;
(2)设购买A型钢板m块,则购买B型钢板(100-m)块,根据“需C型钢板至多150块,D型钢板不超过170块”列出不等式组并解答;
(3)设A型钢板a块,B型钢板b块,由“需C型钢板80块,D型钢板不多于45块”列出不等式组,即可求解.
(1)设用A型钢板x块,用B型钢板y块,
则![]() ,
,
解得:![]() ,
,
答:用A型钢板40块、B型钢板70块;
(2)设A型钢板m块,B型钢板(100﹣m)块,
 ,
,
∴30≤m≤50,
∴共21种方案;
(3)设A型钢板a块,B型钢板b块,
![]() ,
,
∴![]() ,
,
∵b=80﹣2a>0,
∴a<40,
∴![]() ,
,
∴a=39,b=2
∴A型钢板39块,B型钢板2块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB于D,点E为AC上一动点,过点E作EF⊥AB于F,连接DE.
(1)若∠1=∠2,求证:DE∥BC;
(2)在点E运动过程中,直线DE与直线BC交于点M,若∠DCB=α,∠M=β,则∠FED的度为 (用含α,β的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.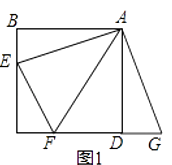
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;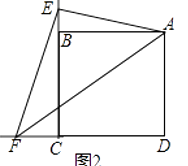
(2)【联想拓展】如图4,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,tan∠ABC=
 ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则
,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则 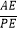 的值为( )
的值为( )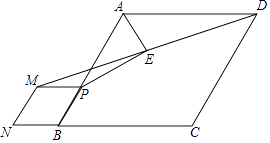
A.
B.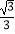
C.
D.
-
科目: 来源: 题型:
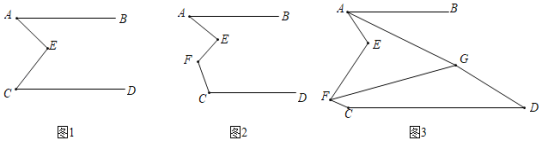
查看答案和解析>>【题目】如图,AB∥CD.
(1)如图1,∠A、∠E、∠C的数量关系为 .
(2)如图2,若∠A=50°,∠F=115°,求∠C﹣∠E的度数;
(3)如图3,∠E=90°,AG,FG分别平分∠BAE,∠CFE,若GD∥FC,试探究∠AGF与∠GDC的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )
A.1
B.
C.
D.
相关试题

