【题目】如图,在Rt△ABC中,∠C=90°,AC=10,BC=15,点D,E,P分别是边AC,AB;BC上的点,且AD=4,AE=4EB.若![]() 是等腰三角形,则CP的长是__________.
是等腰三角形,则CP的长是__________.

参考答案:
【答案】![]() 或
或![]()
【解析】
建立如图平面直角坐标系,,表示出D(0,6)P(x,0)E(12,2),利用长度公式进行分类讨论即可.
建立如图平面直角坐标系
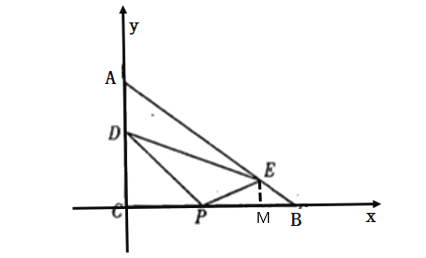
∵AC=10,AD=4
∴![]()
∴![]()
∵过E作EM⊥BC于M
∴EM∥AC
∴![]()
∴BM=3,EM=2
∴CM=12
∴E(12,2)
设P(x,0)
∵AD=4,AC=10
∴CD=6
∵D(0,6)P(x,0)E(12,2)
∴![]() ,
,![]() ,
,![]()
当DE=PD时,![]()
∴![]()
∴![]()
∴![]()
∴CP=![]()
当DE=PE时,![]()
∴![]()
∴![]() (负值舍去)
(负值舍去)
∴![]() >CB
>CB
∵P是边BC上的点
∴当DE=PE时,不符合题意;舍去
当DP=PE时,![]()
∴![]()
∴![]()
∴CP=![]()
故答案为: ![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边在坐标轴上,顶点B落在第一象限,反比例函数
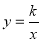 (x>0)的图象经过正方形OABC的中心P,把反比例函数
(x>0)的图象经过正方形OABC的中心P,把反比例函数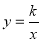 (x>0)的图象向左平移a个单位长度后经过点A,若正方形OABC的边长为4,则a的值为( )
(x>0)的图象向左平移a个单位长度后经过点A,若正方形OABC的边长为4,则a的值为( )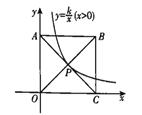
A.
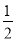 B.1C.
B.1C.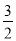 D.2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则
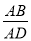 的值是( )
的值是( )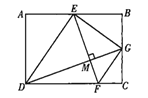
A.
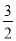 B.
B.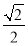 C.
C.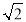 D.
D.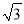
-
科目: 来源: 题型:
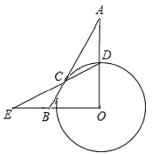
查看答案和解析>>【题目】如图,Rt△AOB的斜边AB切⊙O于点C,OA交⊙O于点D,连接DC并延长交OB的延长线于点E.已知∠A=∠E,若AB=6,则BC的长为__________.
-
科目: 来源: 题型:
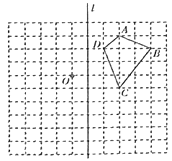
查看答案和解析>>【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形
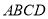 (顶点是网格线的交点).
(顶点是网格线的交点).(1)请画出四边形
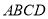 关于直线
关于直线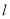 对称的四边形
对称的四边形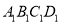 (点
(点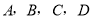 的对应点分别为点
的对应点分别为点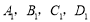 );
);(2)若以点
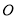 为位似中心,将四边形
为位似中心,将四边形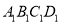 放大到原来的2倍,请在该网格中画出放大后的四边形
放大到原来的2倍,请在该网格中画出放大后的四边形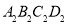 (点
(点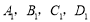 的对应点分别为点
的对应点分别为点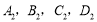 );
);(3)填空:
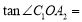 __________.
__________.
-
科目: 来源: 题型:
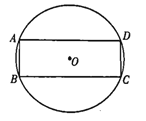
查看答案和解析>>【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
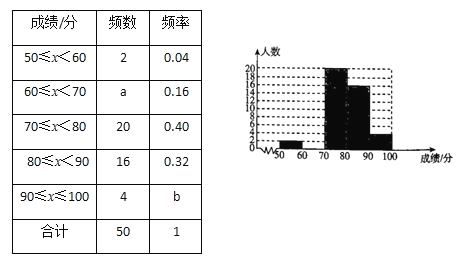
请你根据图表提供的信息,解答下列问题:
(1)求出a,b的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:A.50≤x<60;B.60≤x<80;C.80≤x≤100.若按照这样的分组方式绘制扇形统计图,则其中C组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
相关试题

