搜索
【题目】如图，正方形
内有两点
、
满足
，
，
，
，则正方形的边长为（ ）
A.
B.
C.20D.
参考答案：
【答案】B
【解析】
连接AC，交EF于点M，可证明△AEM∽△CMF，根据条件可求得AE、EM、FM、CF，再结合勾股定理可求得AB.
解：连接AC，交EF于点M，
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF，
∴△AEM∽△CFM，
∴
，
∵AE=4，EF=FC=12，
∴
∴EM=3，FM=9，
在Rt△AEM中，AM2=AE2+EM2=16+9=25，解得AM=5，
在Rt△FCM中，CM2=CF2+FM2=144+81=225，解得CM=15，
∴AC=AM+CM=5+15=20，
在Rt△ABC中，AB=BC，
AB2+BC2=AC2=400
AB2=200
∴AB=10
，即正方形的边长为10．
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．
如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B；…
设游戏者从圈A起跳．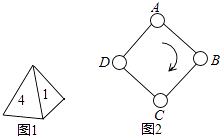
（1）嘉嘉随机掷一次骰子，求落回到圈A的概率P1；
（2）淇淇随机掷两次骰子，用列表法求最后落回到圈A的概率P2 ， 并指出她与嘉嘉落回到圈A的可能性一样吗？ -
科目： 来源： 题型：
查看答案和解析>>【题目】为发展电信事业，方便用户，电信公司对移动电话采取不同的收费方式，其中，所使用的“便民卡”与“如意卡”在某市范围内每月（30天）的通话时间x（min）与通话费y（元）的关系如图所示：
（1）分别求出通话费y1 ， y2与通话时间x之间的函数关系式；
（2）请帮用户计算，在一个月内使用哪一种卡便宜． -
科目： 来源： 题型：
查看答案和解析>>【题目】学校计划在某商店购买秋季运动会的奖品，若买5个篮球和10个足球需花费1150元，若买9个篮球和6个足球需花费1170元.
（1）篮球和足球的单价各是多少元？
（2）实际购买时，正逢该商店进行促销.所有体育用品都按原价的八折优惠出售，学校购买了若干个篮球和足球，恰好花费1760元.请直接写出学校购买篮球和足球的个数各是多少.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一种某小区的两幢10层住宅楼间的距离为AC=30m，由地面向上依次为第1层、第2层、…、第10层，每层高度为3m．假设某一时刻甲楼在乙楼侧面的影长EC=h，太阳光线与水平线的夹角为α
（1）用含α的式子表示h（不必指出α的取值范围）；
（2）用含α的式子表示h（不必指出α的取值范围）； -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥CD，则∠A、∠C、∠E、∠F满足的数量关系是( )
A. ∠A＝∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F＝180°
C. ∠A﹣∠E+∠C+∠F＝90° D. ∠A+∠E+∠C+∠F＝360°
-
科目： 来源： 题型：
查看答案和解析>>【题目】中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
30
0.15
70≤x＜80
40
n
80≤x＜90
m
0.35
90≤x≤100
50
0.25
请根据所给信息，解答下列问题：
(1)m＝ ，n＝ ；
(2)请补全频数分布直方图；
(3)若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
相关试题
