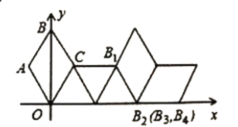
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴正方向无滑动翻转,每次转60°,连续翻转2019次,点B的落点依次为![]() ,则
,则![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
连接AC,根据条件可以求出AC,可推出没翻转6次,图形向右平移4,由于2019=336×6+3,因此点![]() 向右平移1344(即336×4)即可到达点
向右平移1344(即336×4)即可到达点![]() ,根据点
,根据点![]() 的坐标就可以求出点
的坐标就可以求出点![]() 的坐标.
的坐标.
连接AC,如图所示,
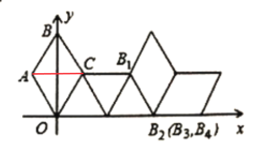
∵四边形OABC是菱形,
∴OA=AB=BC=OC,
∵![]() ,
,
∴△ABC是等边三角形,
∴AC=AB,
∴AC=OA,
∵OA=1,
∴AC=1,
由规律可推出每翻转6次,图形向右平移4,
∵2019=336×6+3,
∴点![]() 向右平移1344(即336×4)即可到达点
向右平移1344(即336×4)即可到达点![]() ,
,
∵![]() 的坐标为(2,0),
的坐标为(2,0),
∴![]() 的坐标为(2+1344,0),
的坐标为(2+1344,0),
∴![]() 的坐标为(1346,0).
的坐标为(1346,0).
故答案选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长10cm,宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使无盖长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的侧面积(指的是高为剪去的正方形边长的长方体的侧面积)可以达到30cm2吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?答:我抽取的2张卡片是________、________,乘积的最大值为________.
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?答:我抽取的2张卡片是________、________,商的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数y=﹣
 x+2的图象分别与x轴、y轴交于点A、B.
x+2的图象分别与x轴、y轴交于点A、B.(1)请直接写出A,B两点坐标:A 、B
(2)在直角坐标系中画出函数图象;
(3)若平面内有一点C(5,3),请连接AC、BC,则△ABC是 三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).
x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).(1)求抛物线的解析式;
(2)求抛物线的顶点坐标及点B的坐标;
(3)设抛物线的对称轴与x轴交于点D,连接CD,并延长CD交抛物线于点E,连接AC,AE,求△ACE的面积;
(4)抛物线上有一个动点M,与A,B两点构成△ABM,是否存在S△ADM=
 S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.
S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.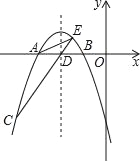
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,延长AB到点C,使得2BC=3OB,D是⊙O上一点,连接AD,CD,过点A作CD的垂线,交CD的延长线于点F,过点D作DE⊥AC于点E,且DE=DF.
(1)求证:CD是⊙O的切线;
(2)若AB=4.
①求DF的长;
②连接OF,交AD于点M,求DM的长.

相关试题

