【题目】如图,AB是⊙O的直径,延长AB到点C,使得2BC=3OB,D是⊙O上一点,连接AD,CD,过点A作CD的垂线,交CD的延长线于点F,过点D作DE⊥AC于点E,且DE=DF.
(1)求证:CD是⊙O的切线;
(2)若AB=4.
①求DF的长;
②连接OF,交AD于点M,求DM的长.

参考答案:
【答案】(1)证明见解析;(2)①DF的长为![]() ;②DM的长为
;②DM的长为![]() .
.
【解析】试题分析:(1)连接OD,根据 DF⊥AF,DE⊥AC,DF=DE,可得∠DAE=∠DAF,由OA=OD,得∠OAD=∠DOA,再根据∠DAF+∠ADF=90°,从而得∠ODA+∠ADF=90°,从而问题得证;
(2)①由已知可得半径OA=OB=2,再根据2BC=3OB,求得BC=3,再利用三角形的面积即可得DE的长;
②由OD∥AF,得![]() ,再根据OC=5,CA=7,AD=AM+DM,从而可得
,再根据OC=5,CA=7,AD=AM+DM,从而可得![]() ,在Rt△ODE中,求出OE长,在Rt△ADE中,求出AD长,从而可得DM长.
,在Rt△ODE中,求出OE长,在Rt△ADE中,求出AD长,从而可得DM长.
试题解析:(1)如图,连接OD.
∵DF⊥AF,DE⊥AC,DF=DE,
∴∠DAE=∠DAF,
∵OA=OD,
∴∠OAD=∠DOA,
∵∠DAF+∠ADF=90°,
∴∠ODA+∠ADF=90°,
∴∠ODF=90°,
∴OD⊥CF,
∴CD是⊙O的切线.
(2)①∵AB=4,
∴OA=OB=2,
∵2BC=3OB,
∴BC=3,
在Rt△OCD中,CD=![]() ,
,
∵![]() OCDE=
OCDE=![]() ODCD,
ODCD,
∴DE=![]() ;
;
②∵OD∥AF,
∴![]() ,
,![]() ,
,
∵OC=5,AC=7,
∴![]() ,∴
,∴![]() ,
,
在Rt△ODE中,OE=![]() =
=![]() ,
,
在Rt△ADE中,AD=![]() ,
,
∴DM=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴正方向无滑动翻转,每次转60°,连续翻转2019次,点B的落点依次为
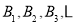 ,则
,则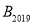 的坐标为( )
的坐标为( )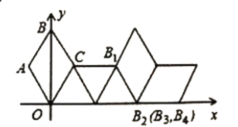
A.
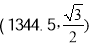 B.
B.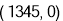
C.
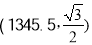 D.
D.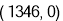
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数y=﹣
 x+2的图象分别与x轴、y轴交于点A、B.
x+2的图象分别与x轴、y轴交于点A、B.(1)请直接写出A,B两点坐标:A 、B
(2)在直角坐标系中画出函数图象;
(3)若平面内有一点C(5,3),请连接AC、BC,则△ABC是 三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).
x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).(1)求抛物线的解析式;
(2)求抛物线的顶点坐标及点B的坐标;
(3)设抛物线的对称轴与x轴交于点D,连接CD,并延长CD交抛物线于点E,连接AC,AE,求△ACE的面积;
(4)抛物线上有一个动点M,与A,B两点构成△ABM,是否存在S△ADM=
 S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.
S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.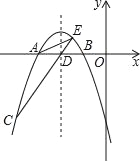
-
科目: 来源: 题型:
查看答案和解析>>【题目】今秋,河北保定易县柿子虽大丰收,却让果农犯了愁.据悉,今年易县有2亿斤柿子滞销,少数乡镇柿子只得4毛钱贱卖,多地柿子无人问津,为解决销路,一家柿子种植大户为村里联系了一个销售渠道,已知有480吨的柿子需运出,某汽车运输公司承办了这次运送任务.
(1)运输公司平均每天运送柿子x吨,需要y天完成运输任务,写出y关于x的函数解析式;
(2)这个公司计划派出4辆卡车,每天共运送32吨.
①求需要多少天完成全部运送任务?
②现需要提前5天运送完毕,需增派同样的卡车多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:


(1)请将右上表补充完整:(参考公式:方差
 )
)(2)请从下列三个不同的角度对这次测试结果进行①从平均数和方差相结合看,__________的成绩好些;②从平均数和中位数相结合看,___________的成绩好些;
(3)若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
相关试题

