【题目】如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
参考答案:
【答案】
(1)解:∵OE为线段BC的中垂线,
∴OC= ![]() BC.
BC.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
![]() ,
,
解得:  ,
,
∴y=﹣ ![]() x2+6
x2+6
(2)解:由题意,得
当y=4.4时,4.4=﹣ ![]() x2+6,
x2+6,
解得:x=± ![]() ,
,
∴宽度为: ![]() >2.4,
>2.4,
∴它能通过该隧道
(3)解:由题意,得
![]() (
( ![]() ﹣0.4)=
﹣0.4)= ![]() ﹣0.2>2.4,
﹣0.2>2.4,
∴该辆货运卡车还能通过隧道
【解析】(1)抛物线的解析式为y=ax2+c,根据E点及D点的坐标由待定系数法就可以求出结论;(2)当y=2.4时代入(1)的解析式求出x的值就求出结论;(3)将(2)求出的宽度﹣0.4m后除以2的值与2.4比较就可以求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有点A(0,4)、B(9,4)、C(12,0)。已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动,运动速度都是每秒一个单位长度,运动时间为t秒.
(1)当四边形AQCB是平行四边形时,求t值;
(2)连接PQ,当四边形APQO是矩形时,求t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层,…,第n层.
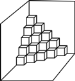
(1)第三层有________个小正方体;
(2)从第四层至第六层(含第四层和第六层)共有________个小正方体;
(3)第n层有________个小正方体;
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为________平方分米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B是线段AD上一动点,沿A→D→A以 2 cm/s的速度往返运动1次,C是线段BD的中点,AD=10 cm,设点B的运动时间为t秒(0≤t≤10).
(1)当t=2时,
①AB=____cm;
②求线段CD的长度;
(2)用含t的代数式表示运动过程中AB的长;
(3)在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )

A.49 B.25 C.13 D.1
相关试题

