Question

【题目】如图是按规律摆放在墙角的一些小正方体，从上往下分别记为第一层，第二层，第三层，…，第n层．

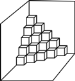
(1)第三层有________个小正方体；

(2)从第四层至第六层(含第四层和第六层)共有________个小正方体；

(3)第n层有________个小正方体；

(4)若每个小正方体边长为a分米，共摆放了n层，则要将摆放的小正方体能看到的表面部分涂上防锈漆，则防锈漆的总面积为________平方分米．

Answer 1

【答案】（1）6（2）46（3） （4）a2n(n＋1)

【解析】

（1）第1个图有1层，共1个小正方体，第2个图有2层，第2层正方体的个数为1+2，以此类推第三层即可；

（2）第4至6层求出每层个数相加即可；

（3）根据相应规律可得第n层正方体的个数为1+2+3+…+n= ；

（4）共摆放n层，根据正面、右面、上面小正方形的面的个数，求出总面数再乘每一个小正方形的面积即可．

解：（1）第1层，共1个小正方体，

第2层正方体的个数为1+2=3，

第3层正方体的个数为：1+2+3=6．

故答案为：6．

（2）第4层正方体的个数为：10，

第5层正方体的个数为：15，

第6层正方体的个数为：21，

所以从第四层至第六层（含第四层和第六层）共有：10+15+21=46．

故答案为：46．

（3）根据（1）相应规律，可得第n层正方体的个数为1+2+3+…+n=；

（4）共摆放n层，则正面小正方形的面的个数：2×（1+2+3+…+n）=n（n+1），

右面小正方形的面的个数：1+2+3+…+n=，

所以涂上防锈漆的面积为：[n（n+1）+]×a2=a2n（n+1）分米2．

故答案为：（1）6；（2）41；（3）；（4）a2n（n+1）．