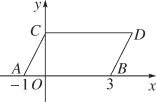
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将A,B两点向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)若点P在直线BD上运动,连接PC,PO.
①若点P在线段BD上(不与B,D重合)时,求S△CDP+S△BOP的取值范围;
②若点P在直线BD上运动,试探索∠CPO,∠DCP,∠BOP的关系,并证明你的结论.
参考答案:
【答案】(1)由平移可知点C的坐标为(0,2),点D的坐标为(4,2);(2)①3<S△CDP+S△BOP<4;②当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点
;当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ;当点
;当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() .
.
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加求出![]() 、
、![]() 的坐标即可;
的坐标即可;
(2)①设点![]() 的纵坐标为
的纵坐标为![]() ,将
,将![]() 与
与![]() 的面积表示出来,从而得到
的面积表示出来,从而得到![]() ,根据题可知
,根据题可知![]() ,即可得到
,即可得到![]() 的范围;
的范围;
②分三种情况,根据平移的性质可得![]() ,再过点
,再过点![]() 作
作![]() ,根据平行公理可得
,根据平行公理可得![]() ,然后根据两直线平行,内错角相等可得
,然后根据两直线平行,内错角相等可得![]() ,
,![]() 即可得到结论.
即可得到结论.
(1)由平移可知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)①设点![]() 的纵坐标为
的纵坐标为![]() ,
,
![]() 点
点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,易知
,易知![]() ,
,![]() ,
,![]() ,
,![]() 轴,
轴,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
②当点![]() 在线段
在线段![]() 上时,如图1
上时,如图1
由平移的性质得,![]() ,
,
过点![]() 作
作![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
由平移的性质得,![]() ,
,
点![]() 作
作![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当点![]() 在线段
在线段![]() 的延长线上时,如图3,
的延长线上时,如图3,
同(2)的方法得出![]() .
.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】望江中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽取了部分学生进行调查统计,并将调查统计的结果分为以下四类:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)m=________%,n=________%,这次共抽取了________名学生进行调查统计;
(2)请补全上面的条形图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机张师傅某天上午营运全是在东西向的长江路上进行的,如果向东为正,向西为负,这天上午他行车里程(单位:km)如下:
 .
.⑴.最后一名乘客送到目的地,出租车在东面还是西面?在多少千米处?
⑵.请你帮张师傅算一下,这天上午他一共行驶了多少里程?
⑶.若每千米耗油0.1L,则这天上午张师傅一共用了多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若
 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.(3)若
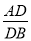 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).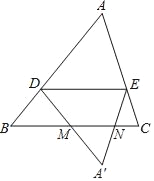
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
相关试题

