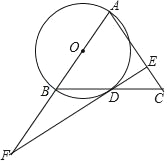
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC交AC于点E,延长ED交AB的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若AB=8,AE=6,求BF的长.
参考答案:
【答案】(1)证明见解析;(2)4
【解析】分析:(1)连接OD,根据等腰三角形的性质得到∠ABC=∠C,∠ABC=∠ODB,证明OD∥AC,根据平行线的性质得到OD⊥DE,根据切线的判定定理证明;
(2)证明△FOD∽△FAE,根据相似三角形的性质定理列出比例式,计算即可.
详(1)证明:连接OD,
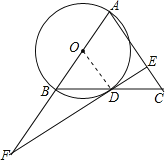
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,又DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OD∥AC,
∴△FOD∽△FAE,
∴![]() ,即
,即![]() ,
,
解得,BF=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验中学八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
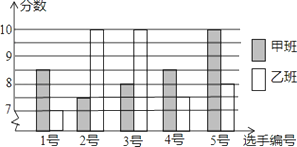
(1)根据上图填写下表:
平均数
中位数
众数
方差
甲班
8.5
8.5
______
______
乙班
8.5
_____
10
1.6
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
-
科目: 来源: 题型:
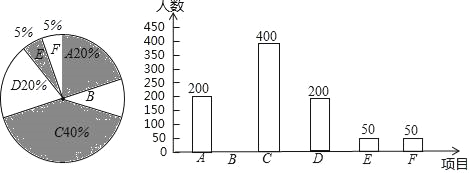
查看答案和解析>>【题目】电视热播节目“最强大脑”激发了学生的思考兴趣,为满足学生的需求,某学校抽取部分学生举行“最强大脑”选拔赛,针对竞赛成绩分成以下六个等级A:0~50分;B:51~60分;C:61~70分;D:71~80分;E:81~90分;F:91~100分,根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
(1)此次竞赛抽取的总人数为 ,请补全条形统计图;
(2)若全市约有3万名在校学生,试估计全市学生中竞赛成绩在71~90分的人数约有多少?
(3)若在此次接受调查的学生中,随机抽查一人,则此人的成绩在80分以上的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
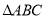 是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.
是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.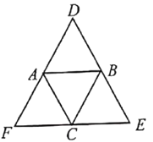
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作
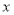 、
、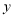 ,把
,把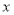 、
、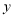 作为点
作为点 的横、纵坐标.
的横、纵坐标.
(1)写出点
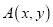 所有可能的坐标;
所有可能的坐标;(2)求点
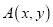 在直线
在直线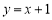 上的概率.
上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】位于河南省郑州市的炎黄二帝巨型塑像,是为代表中华民族之创始、之和谐、之统一.塑像由山体CD和头像AD两部分组成.某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°,头像A处的仰角为70.5°,求头像AD的高度.(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
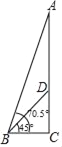
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若a,b互为相反数,则
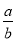 =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为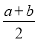 分.其中正确的为____(填序号).
分.其中正确的为____(填序号).
相关试题

