【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 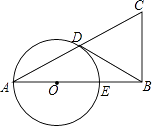
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
参考答案:
【答案】
(1)证明:连接DE,
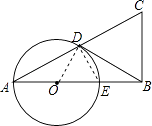
∵AE是直径,
∴∠ADE=90°,
∴∠ADE=∠ABC,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ ![]() ,
,
∴ACAD=ABAE
(2)解:连接OD,

∵BD是⊙O的切线,
∴OD⊥BD,
在RT△OBD中,OE=BE=OD,
∴OB=2OD,
∴∠OBD=30°,
同理∠BAC=30°,
在RT△ABC中,AC=2BC=2×2=4
【解析】(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
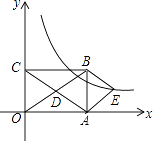
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式. -
科目: 来源: 题型:
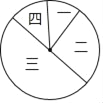
查看答案和解析>>【题目】如图,一、二、三、四这四个扇形的面积之比为1:3:5:1.
(1)请分别求出它们圆心角的度数.
(2)一、二、四这三个扇形的圆心角的度数之和是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了一元一次方程的解法,下面是小明同学的解题过程:
解方程

解:方程两边同时乘以6,得:
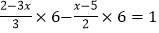 …①
…①去分母,得:2(2﹣3x)﹣3(x﹣5)=1…②
去括号,得:4﹣6x﹣3x+15=1…③
移项,得:﹣6x﹣3x=1﹣4﹣15…④
合并同类项,得:﹣9x=﹣18…⑤
系数化1,得:x=2…⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x(x≥0)与双曲线y=
 (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为 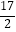 m.
m. 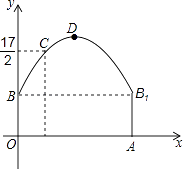
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
相关试题

