【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣ ![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为 ![]() m.
m. 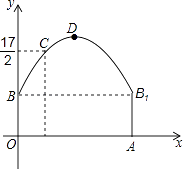
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
参考答案:
【答案】
(1)解:根据题意得B(0,4),C(3, ![]() ),
),
把B(0,4),C(3, ![]() )代入y=﹣
)代入y=﹣ ![]() x2+bx+c得
x2+bx+c得 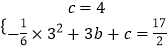 ,
,
解得 ![]() .
.
所以抛物线解析式为y=﹣ ![]() x2+2x+4,
x2+2x+4,
则y=﹣ ![]() (x﹣6)2+10,
(x﹣6)2+10,
所以D(6,10),
所以拱顶D到地面OA的距离为10m
(2)解:由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= ![]() >6,
>6,
所以这辆货车能安全通过
(3)解:令y=8,则﹣ ![]() (x﹣6)2+10=8,解得x1=6+2
(x﹣6)2+10=8,解得x1=6+2 ![]() ,x2=6﹣2
,x2=6﹣2 ![]() ,
,
则x1﹣x2=4 ![]() ,
,
所以两排灯的水平距离最小是4 ![]() m
m
【解析】(1)先确定B点和C点坐标,然后利用待定系数法求出抛物线解析式,再利用配方法确定顶点D的坐标,从而得到点D到地面OA的距离;(2)由于抛物线的对称轴为直线x=6,而隧道内设双向行车道,车宽为4m,则货运汽车最外侧与地面OA的交点为(2,0)或(10,0),然后计算自变量为2或10的函数值,再把函数值与6进行大小比较即可判断;(3)抛物线开口向下,函数值越大,对称点之间的距离越小,于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
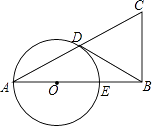
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了一元一次方程的解法,下面是小明同学的解题过程:
解方程

解:方程两边同时乘以6,得:
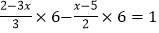 …①
…①去分母,得:2(2﹣3x)﹣3(x﹣5)=1…②
去括号,得:4﹣6x﹣3x+15=1…③
移项,得:﹣6x﹣3x=1﹣4﹣15…④
合并同类项,得:﹣9x=﹣18…⑤
系数化1,得:x=2…⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x(x≥0)与双曲线y=
 (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

-
科目: 来源: 题型:
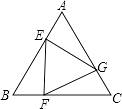
查看答案和解析>>【题目】如图,已知等边三角形ABC的边长为2,E、F、G分别是边AB、BC、CA的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y与x的函数图象大致是( )
A.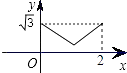
B.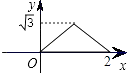
C.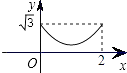
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠ACB=90°,点E为△ABC内一点,且∠BEC=90°,将△BEC绕C点顺时针旋转90°,使BC与AC重合,得到△AFC,连接EF交AC于点M,已知BC=10,CF=6,则AM:MC的值为( )
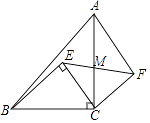
A.4:3
B.3:4
C.5:3
D.3:5 -
科目: 来源: 题型:
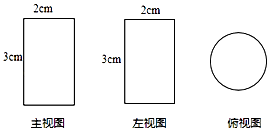
查看答案和解析>>【题目】一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为 .
相关试题

