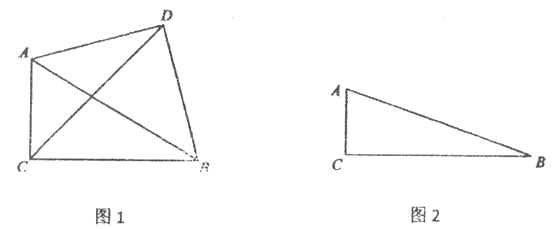
【题目】在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
参考答案:
【答案】(1)105°;(2)①答案见解析;②CD=2![]() ;(3)AC+BC=
;(3)AC+BC=![]() CD.
CD.
【解析】试题分析:(1)先判断出∠CAD=∠DBE,再利用等腰直角三角形求出∠ABD=45°,进而求出∠CBD,最后用邻补角即可得出结论;
(2)①根据题意及基本作图即可补全图形;
②构造出△ACD≌△BED,进而判断出△CDE是等腰直角三角形,再利用等腰直角三角形的性质即可得出解;
构造出△BDH≌△ADG,进而判断出△CDH是等腰直角三角形,再利用等腰直角三角形的性质即可得出结论;
(3)同(2)的方法即可得出结论.
试题解析:
(1)∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵△ADB是等腰直角三角形,
∴∠ABD=45°,
∵∠ABC=30°,
∴∠CBD=∠ABD+∠ABC=75°,
∴∠CAD=∠DBE=180°-75°=105°
故答案为:105°.
(2)①补全图形,如图所示.
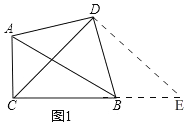
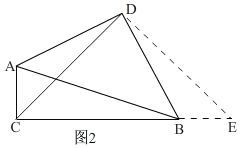
②如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∴CD=2![]() .
.
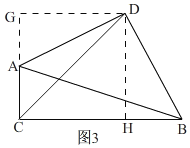
如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DAG+∠CAD═180°,
∴∠CBD=∠DAG.
∵DA=DB,∠DGA=∠DHB=90°,
∴△BDH≌△ADG.
∴DH=DG,BH=AG.
∴∠DCH=∠DCG=45°.
∴△CHD为等腰直角三角形.
∵AC=1,BC=3,
∴CH=2.
∴CD=2![]() .
.
(3)AC+BC=![]() CD,
CD,
理由:如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE=![]() CD,
CD,
∵CE=BC+BE=BC+AC.
即:AC+BC=![]() CD.
CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若八个数据x1, x2, x3, ……x8, 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1, x2, x3, …x8;8的平均数
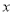 ________8,方差为S2 ________1.(填“>”、“=”、“<”)
________8,方差为S2 ________1.(填“>”、“=”、“<”) -
科目: 来源: 题型:
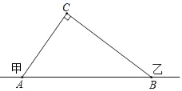
查看答案和解析>>【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,M,N,P,R分别是数轴上的四个整数所对应的点,其中有一个点是原点,并且,MN=NP=PR=1,数a对应的点在M和N之间,数b对应的点在P和R之间,若|a|+|b|=2,则原点是(填M,N,P,R中的一个或几个)_____________

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有 5 张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:

(1)从中取出 2 张卡片,使这 2 张卡片上数字的乘积最大,乘积的最大值为 ;
(2)从中取出 2 张卡片,使这 2 张卡片上数字相除的商最小,商的最小值为 ;
(3)从中取出 4 张卡片,用学过的运算方法,使结果为 24.写出运算式子.(写出一种即可)算 24 的式子为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
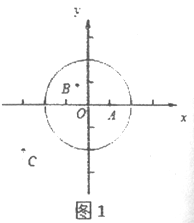
A(1,0)的距离跨度______________;
B(-
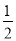 ,
, 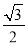 )的距离跨度____________;
)的距离跨度____________;C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
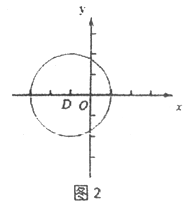
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
(3)如图3,在平面直角坐标系xOy中,射线OP:y=
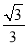 x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.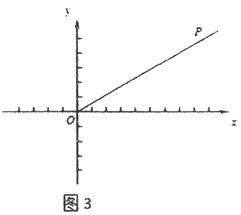
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将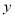 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
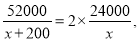 解得
解得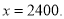
经检验,
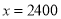 是原方程的解.
是原方程的解.答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
 解得
解得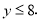
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,
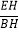 =3时,求
=3时,求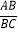 的值.
的值.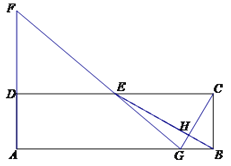
相关试题

