【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为( ![]() ,
, ![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= ![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: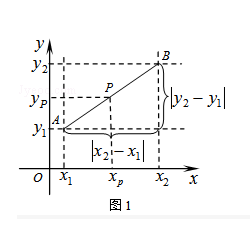
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.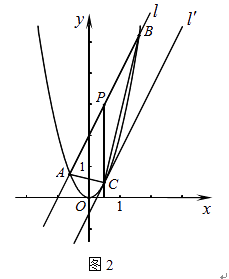
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
参考答案:
【答案】
(1)(0,0);2 ![]()
(2)
解:(a)联立直线、抛物线,得 ![]() ,
,
解得 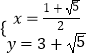 ,
, 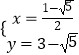 ,
,
即B( ![]() ,3+
,3+ ![]() ),A(
),A( ![]() ,3﹣
,3﹣ ![]() ).
).
由P是AB的中点,得
P( ![]() ,3)
,3)
当x= ![]() 时,y=2x2=
时,y=2x2= ![]() ,即C点坐标为(
,即C点坐标为( ![]() ,
, ![]() ).
).
(b)AB2=( ![]() ﹣
﹣ ![]() )2+(3+
)2+(3+ ![]() ﹣3+
﹣3+ ![]() )2=25;
)2=25;
BC2=( ![]() ﹣
﹣ ![]() )2+(3+
)2+(3+ ![]() ﹣
﹣ ![]() )2=
)2= ![]() ﹣5
﹣5 ![]() ;
;
AC2=( ![]() ﹣
﹣ ![]() )2+(3﹣
)2+(3﹣ ![]() ﹣
﹣ ![]() )2=
)2= ![]() +5
+5 ![]() ,
,
∵AC2+BC2=AB2,
∴∠ACB=90°
∴△ABC是直角三角形;
(c)如图 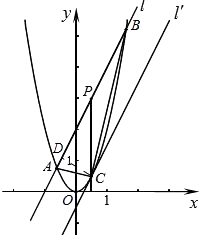 ,
,
作CD⊥AB于D点,CD 是两直线间的距离,
S△ABC= ![]() ABCD=
ABCD= ![]() ACBC,
ACBC,
![]() ×5CD=
×5CD= ![]() ×
× ![]() ,
,
解得CD= ![]() .
.
两直线l与l′的距离是 ![]()
【解析】解:(1)由中点坐标,得 ![]() =0,
=0, ![]() =0,
=0,
MN中点坐标为(0,0),
由两点间的距离,得
MN= ![]() =2
=2 ![]() ,
,
所以答案是:(0,0),2 ![]() .
.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线C1:
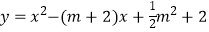 与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
(1)求m,n的值;
(2)试写出x为何值时,y1>y2?
(3)试描述抛物线C1通过怎样的变换得到抛物线C2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
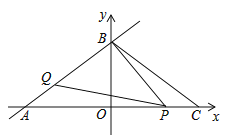
查看答案和解析>>【题目】如图,直线
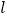 :
: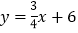 交
交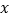 、
、 轴分别为
轴分别为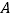 、
、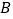 两点,
两点,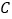 点与
点与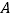 点关于
点关于 轴对称.动点
轴对称.动点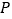 、
、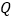 分别在线段
分别在线段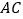 、
、 上(点
上(点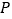 不与点
不与点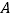 、
、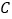 重合),满足
重合),满足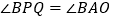 .
.
(1)点
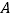 坐标是 ,
坐标是 ,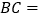 .
.(2)当点
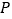 在什么位置时,
在什么位置时,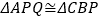 ,说明理由.
,说明理由.(3)当
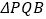 为等腰三角形时,求点
为等腰三角形时,求点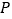 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
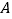 ,
,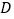 分别在
分别在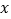 轴,
轴,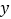 轴上,
轴上,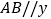 轴,
轴,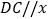 轴.点
轴.点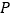 从点
从点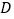 出发,以1个单位长度/秒的速度,沿五边形
出发,以1个单位长度/秒的速度,沿五边形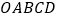 的边顺时针匀速运动一周,若顺次连接
的边顺时针匀速运动一周,若顺次连接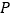 ,
,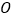 ,
,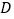 三点所围成的三角形的面积为
三点所围成的三角形的面积为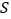 ,点
,点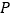 运动的时间为
运动的时间为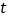 秒,已知
秒,已知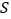 与
与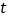 之间的函数关系如图②中折线
之间的函数关系如图②中折线 所示.
所示.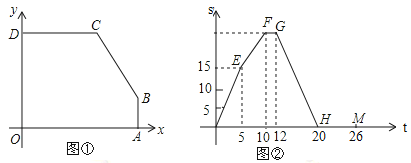
(1)图①中点
 的坐标为 ;点
的坐标为 ;点 的坐标为 ;
的坐标为 ;(2)求图②中
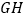 所在直线的解析式;
所在直线的解析式;(3)是否存在点
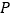 ,使
,使 的面积为五边形
的面积为五边形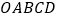 的面积的
的面积的 ?若存在,请求出点
?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
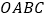 是一张放在平面直角坐标系中的长方形纸片,
是一张放在平面直角坐标系中的长方形纸片,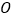 为原点,点
为原点,点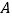 在
在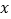 轴的正半轴上,点
轴的正半轴上,点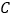 在
在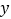 轴的正半轴上,
轴的正半轴上,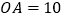 ,
,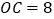 .在
.在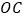 边上取一点
边上取一点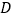 ,将纸片沿
,将纸片沿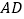 翻折,使点
翻折,使点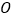 落在
落在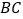 边上的点
边上的点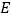 处.
处.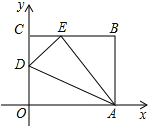
(1)求
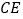 和
和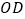 的长;
的长;(2)求直线
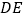 的表达式;
的表达式;(3)直线
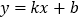 与
与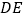 平行,当它与矩形
平行,当它与矩形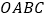 有公共点时,直接写出
有公共点时,直接写出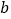 的取值范围.
的取值范围.
相关试题

