【题目】已知:抛物线C1: ![]() 与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
(1)求m,n的值;
(2)试写出x为何值时,y1>y2?
(3)试描述抛物线C1通过怎样的变换得到抛物线C2 .
参考答案:
【答案】
(1)
解:由C1知:△=(m+2)2﹣4×( ![]() m2+2)=m2+4m+4﹣2m2﹣8=﹣m2+4m﹣4=﹣(m﹣2)2≥0,
m2+2)=m2+4m+4﹣2m2﹣8=﹣m2+4m﹣4=﹣(m﹣2)2≥0,
∴m=2.
当x=0时,y=4.∴当x=0时,n=4
(2)
解:令y1>y2时,x2﹣4x+4>x2+4x+4,
∴x<0.
∴当x<0时,y1>y2
(3)
解:由C1向左平移4个单位长度得到C2
【解析】(1)由于两函数都与x轴有交点,可令抛物线C1中,y=0,得出的方程必有△≥0,时,据此可求出的m的值,由于两函数与y轴的交点相同,可先根据C1求出与y轴的交点,然后代入C2中即可求出n的值.(2)根据(1)可得出两函数的解析式,令y1>y2 , 可得出一个不等式方程,即可求出x的取值范围.(3)将两函数化为顶点式,即可得出所求的结论.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
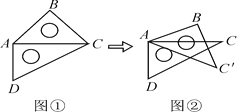
查看答案和解析>>【题目】取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′,如图②所示.设∠CAC′=α(0°<α≤45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化,若变化 ,求出变化范围;若不变,求出其度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
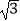 ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).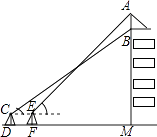
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
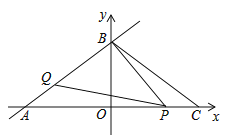
查看答案和解析>>【题目】如图,直线
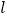 :
: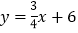 交
交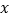 、
、 轴分别为
轴分别为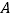 、
、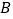 两点,
两点,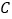 点与
点与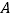 点关于
点关于 轴对称.动点
轴对称.动点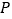 、
、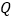 分别在线段
分别在线段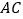 、
、 上(点
上(点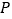 不与点
不与点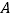 、
、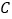 重合),满足
重合),满足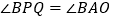 .
.
(1)点
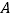 坐标是 ,
坐标是 ,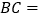 .
.(2)当点
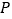 在什么位置时,
在什么位置时,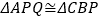 ,说明理由.
,说明理由.(3)当
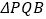 为等腰三角形时,求点
为等腰三角形时,求点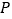 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp=
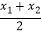 ,同理yp=
,同理yp= 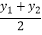 ,所以AB的中点坐标为(
,所以AB的中点坐标为( 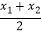 ,
, 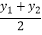 ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= 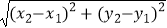 .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: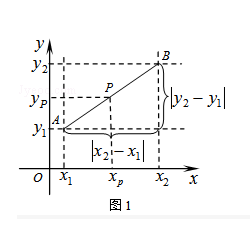
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.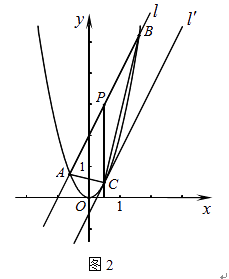
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
相关试题

