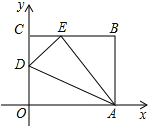
【题目】如图,四边形![]() 是一张放在平面直角坐标系中的长方形纸片,
是一张放在平面直角坐标系中的长方形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .在
.在![]() 边上取一点
边上取一点![]() ,将纸片沿
,将纸片沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
(1)求![]() 和
和![]() 的长;
的长;
(2)求直线![]() 的表达式;
的表达式;
(3)直线![]() 与
与![]() 平行,当它与矩形
平行,当它与矩形![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据勾股定理求出BE的长,进而可得出CE的长,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长;
(2)根据CE、OD的长求得D、E的坐标,然后根据待定系数法即可求得表达式;
(3)根据平行的性质分析讨论即可求得.
解:(1)依题意可知,折痕![]() 是四边形
是四边形![]() 的对称轴,
的对称轴,
∴在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,解得
,解得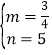 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(3)∵直线![]() 与
与![]() 平行,
平行,
∴直线为![]() ,
,
∴当直线经过![]() 点时,
点时,![]() ,则
,则![]() ,
,
当直线经过![]() 点时,则
点时,则![]() ,
,
∴当直线![]() 与矩形
与矩形![]() 有公共点时,
有公共点时,![]() .
.
故答案为:(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp=
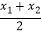 ,同理yp=
,同理yp= 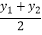 ,所以AB的中点坐标为(
,所以AB的中点坐标为( 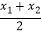 ,
, 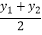 ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= 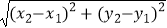 .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: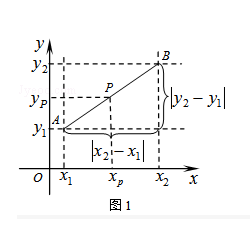
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.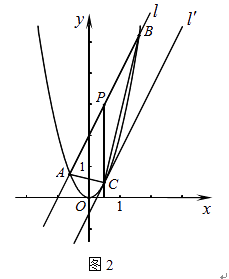
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
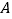 ,
,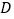 分别在
分别在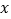 轴,
轴,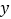 轴上,
轴上,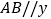 轴,
轴,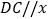 轴.点
轴.点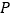 从点
从点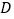 出发,以1个单位长度/秒的速度,沿五边形
出发,以1个单位长度/秒的速度,沿五边形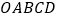 的边顺时针匀速运动一周,若顺次连接
的边顺时针匀速运动一周,若顺次连接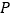 ,
,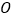 ,
,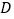 三点所围成的三角形的面积为
三点所围成的三角形的面积为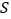 ,点
,点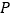 运动的时间为
运动的时间为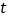 秒,已知
秒,已知 与
与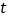 之间的函数关系如图②中折线
之间的函数关系如图②中折线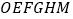 所示.
所示.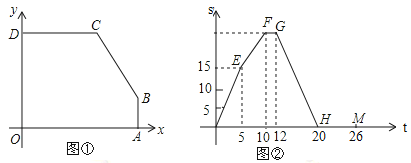
(1)图①中点
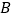 的坐标为 ;点
的坐标为 ;点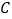 的坐标为 ;
的坐标为 ;(2)求图②中
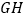 所在直线的解析式;
所在直线的解析式;(3)是否存在点
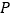 ,使
,使 的面积为五边形
的面积为五边形 的面积的
的面积的 ?若存在,请求出点
?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).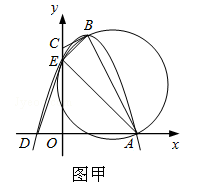
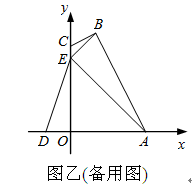
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为 .
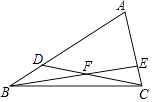
-
科目: 来源: 题型:
查看答案和解析>>【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买
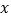 个文具盒,10件奖品共需
个文具盒,10件奖品共需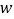 元,求
元,求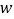 与
与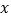 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
相关试题

