Question

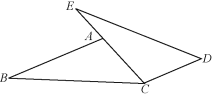
【题目】（1）已知：如图，点E，A，C在同一条直线上，AB∥CD，AB=CE，AC=CD．求证：BC=ED．

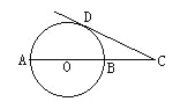
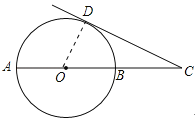
（2）如图，在⊙O中，过直径AB延长线上的点C做⊙O的一条切线，切点为D，若CD=4，CB=2．求：⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）3．

【解析】

试题分析：（1）利用“边边边”证明△ABC和△CED全等，根据全等三角形对应角相等可得∠CAB=∠DCE，再根据内错角相等，两直线平行证明即可；

（2）连接OD，根据切线的性质，∠ODC=90°，设OD=r，在RT△ODC中利用勾股定理即可解决．

试题解析：（1）在△ABC和△CED中，

∵AB=CE，AC=CD，BC=ED，∴△ABC≌△CED（SSS），

∴∠CAB=∠DCE，

∴AB∥CD．

（2）连接OD．

∵CD是⊙O切线，∴OD⊥CD，∴∠ODC=90°，

设半径为r，

在RT△ODC中，∵OD=r，OC=r+2，CD=4，

∴，

∴，

∴r=3，

∴⊙O的半径为3．