【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过点A、C，与AB交于点D．

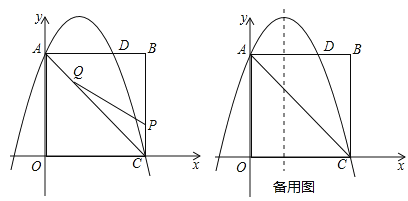
（1）求抛物线的函数解析式；

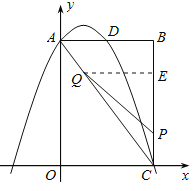
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

①求S关于m的函数表达式；

②当S最大时，在抛物线的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）；（2）①；②（，4），（，8），（，）或（，）．

【解析】

试题分析：（1）将A、C两点坐标代入抛物线，即可求得抛物线的解析式；

（2）①先用m表示出QE的长度，进而求出三角形的面积S关于m的函数；

②直接写出满足条件的F点的坐标即可，注意不要漏写．

试题解析：（1）将A、C两点坐标代入抛物线，得

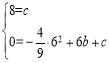，解得：，∴抛物线的解析式为；

（2）①∵OA=8，OC=6，∴AC==10，过点Q作QE⊥BC与E点，则sin∠ACB=，∴，∴QE=，∴S=CPQE=m×=；

②∵S=CPQE=m×==，∴当m=5时，S取最大值；

在抛物线对称轴l上存在点F，使△FDQ为直角三角形，∵抛物线的解析式为的对称轴为x=，D的坐标为（3，8），Q（3，4）；

当∠FDQ=90°时，F1（，8）；

当∠FQD=90°时，则F2（，4）；

当∠DFQ=90°时，设F（，n），则，即，解得：n=，∴F3（，），F4（，），满足条件的点F共有四个，坐标分别为

F1（，8），F2（，4），F3（，），F4（，）．

关闭