【题目】如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
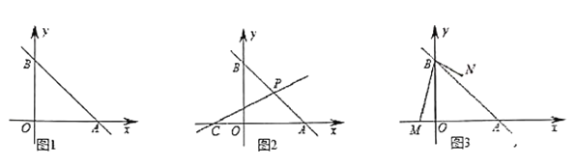
(1)直接写出![]() 的值为______.
的值为______.
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
参考答案:
【答案】(1)k=-1;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)将![]() 代入
代入![]() ,求解即可得出;
,求解即可得出;
(2)先求得直线![]() 为
为![]() ,用含t的式子表示MN,根据
,用含t的式子表示MN,根据![]() 列出方程
列出方程![]() ,分三种情况讨论,可得到
,分三种情况讨论,可得到![]() 或
或![]() ;
;
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,再证出
,再证出![]() ,得到直线
,得到直线![]() 的解析式为
的解析式为![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,可得出
,可得出![]() .
.
解:(1)将![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() .
.
故答案为:![]()
(2)∵在直线![]() 中,令
中,令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴直线![]() 为
为![]() ,
,
∵![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,分情况讨论:
,分情况讨论:
①当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
②当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
③当![]() 时,
时,![]() ,解得:
,解得:![]() ,舍去.
,舍去.
综上所述:![]() 或
或![]() .
.
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,
,
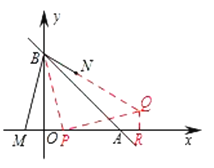
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
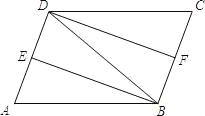
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 的边长为4,
的边长为4, 、
、 分别为直线
分别为直线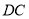 、
、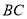 上两点.
上两点.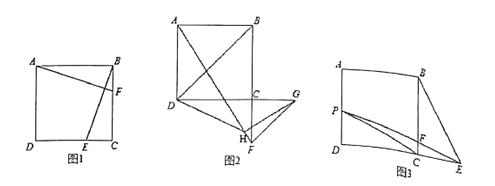
(1)如图1,点
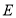 在
在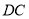 上,点
上,点 在
在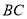 上,
上,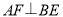 ,求证:
,求证: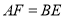 .
.(2)如图2,点
 为
为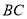 延长线上一点,作
延长线上一点,作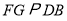 交
交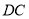 的延长线于
的延长线于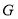 ,作
,作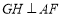 于
于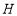 ,求
,求 的长.
的长.(3)如图3,点
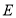 在
在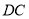 的延长线上,
的延长线上,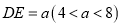 ,点
,点 在
在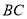 上,
上,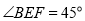 ,直线
,直线 交
交 于
于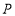 ,连接
,连接 ,设
,设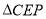 的面积为
的面积为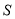 ,直接写出
,直接写出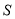 与
与 的函数关系式.
的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
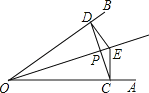
A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以2cm/s和3cm/s的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为( )
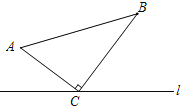
A. 4.6或7B. 7或8C. 4.6或8D. 4.6或7或8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在2015年至2017年期间销售一种礼盒。2015年,该商店用3 500元购进了这种礼盒并且全部售完;2017年,这种礼盒的进价比2015年下降了11元/盒,该商店用2 400元购进了与2015年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2015年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
相关试题

