【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
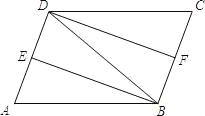
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)首先根据角平分线性质与平行线性质证明∠ABD=∠CDB,再根据平行四边形性质证出CD=AB,∠A=∠C,可利用ASA定理判定△ABE≌△CDF;
(2)根据全等得出AE=CF,根据平行四边形性质得出AD∥BC,AD=BC,推出DE∥BF,DE=BF,得出四边形DFBE是平行四边形,根据等腰三角形性质得出∠DEB=90°,根据矩形的判定推出即可.
试题解析:(1)∵∠ABD的平分线BE交AD于点E,
∴∠ABE=![]() ∠ABD,
∠ABD,
∵∠CDB的平分线DF交BC于点F,
∴∠CDF=![]() ∠CDB,
∠CDB,
∵在平行四边形ABCD中,
∴AB∥CD,
∴∠ABD=∠CDB,
∴∠CDF=∠ABE,
∵四边形ABCD是平行四边形,
∴CD=AB,∠A=∠C,
即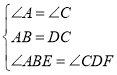 ,
,
∴△ABE≌△CDF(ASA);
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,方格纸中的每个小方格都是边长为1个单位的正方形,
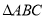 的顶点以及点
的顶点以及点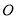 均在格点上.
均在格点上.①直接写出
 的长为______;
的长为______;②画出以
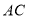 为边,
为边,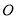 为对角线交点的平行四边形
为对角线交点的平行四边形 .
.(2)如图2,画出一个以
 为对角线,面积为6的矩形
为对角线,面积为6的矩形 ,且
,且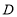 和
和 均在格点上(
均在格点上(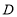 、
、 、
、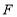 、
、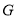 按顺时针方向排列).
按顺时针方向排列).(3)如图3,正方形
 中,
中, 为
为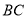 上一点,在线段
上一点,在线段 上找一点
上找一点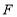 ,使得
,使得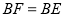 .(要求用无刻度的直尺画图,不准用圆规,不写作法,保留画图痕迹)
.(要求用无刻度的直尺画图,不准用圆规,不写作法,保留画图痕迹)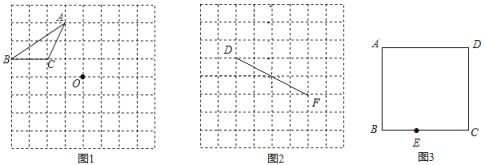
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平画直角坐标系中,直线
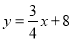 交
交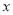 轴于点
轴于点 ,交
,交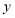 轴于点
轴于点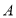 ,将直线
,将直线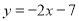 沿
沿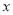 轴向右平移2个单位长度交
轴向右平移2个单位长度交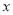 轴于
轴于 ,交
,交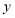 轴于
轴于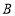 ,交直线
,交直线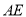 于
于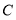 .
.
(1)直接写出直线
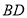 的解析式为______,
的解析式为______,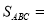 ______.
______.(2)在直线
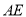 上存在点
上存在点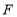 ,使
,使 是
是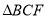 的中线,求点
的中线,求点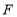 的坐标;
的坐标;(3)如图2,在
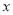 轴正半轴上存在点
轴正半轴上存在点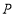 ,使
,使 ,求点
,求点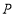 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 的边长为4,
的边长为4,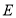 、
、 分别为直线
分别为直线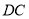 、
、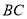 上两点.
上两点.
(1)如图1,点
 在
在 上,点
上,点 在
在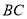 上,
上,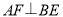 ,求证:
,求证: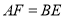 .
.(2)如图2,点
 为
为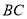 延长线上一点,作
延长线上一点,作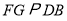 交
交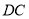 的延长线于
的延长线于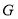 ,作
,作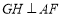 于
于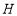 ,求
,求 的长.
的长.(3)如图3,点
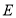 在
在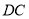 的延长线上,
的延长线上,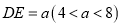 ,点
,点 在
在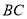 上,
上,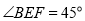 ,直线
,直线 交
交 于
于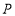 ,连接
,连接 ,设
,设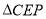 的面积为
的面积为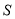 ,直接写出
,直接写出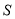 与
与 的函数关系式.
的函数关系式. -
科目: 来源: 题型:
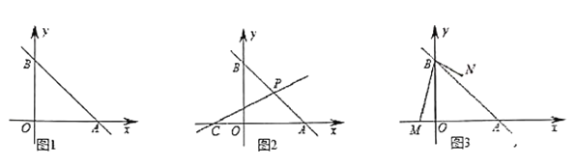
查看答案和解析>>【题目】如图1,已知直线
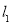 :
: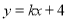 交
交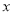 轴于
轴于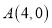 ,交
,交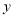 轴于
轴于 .
.
(1)直接写出
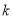 的值为______.
的值为______.(2)如图2,
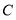 为
为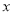 轴负半轴上一点,过
轴负半轴上一点,过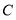 点的直线
点的直线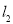 :
: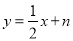 经过
经过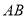 的中点
的中点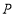 ,点
,点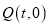 为
为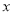 轴上一动点,过
轴上一动点,过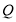 作
作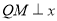 轴分别交直线
轴分别交直线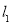 、
、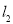 于
于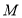 、
、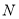 ,且
,且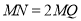 ,求
,求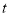 的值.
的值.(3)如图3,已知点
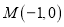 ,点
,点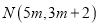 为直线
为直线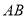 右侧一点,且满足
右侧一点,且满足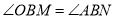 ,求点
,求点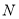 坐标.
坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
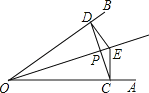
A. 3个B. 4个C. 5个D. 6个
相关试题

