【题目】设![]() 、
、![]() 是抛物线
是抛物线![]() 上的点,坐标系原点
上的点,坐标系原点![]() 位于线段
位于线段![]() 的中点处,则
的中点处,则![]() 的长为_____.
的长为_____.
参考答案:
【答案】2![]()
【解析】
由于原点O是线段AB的中点得到A点和B点关于原点中心对称,则x1=-x2,y1=-y2,根据抛物线的位置可确定A点和B点在第一、三象限,设A点在第一象限,再把点A和B点坐标代入解析式得到y1=2x12+4x1-2,-y1=2x12-4x1-2,两式相加可得x1=1,则y1=4,于是可确定A点和B点坐标,然后利用两点间的距离公式计算.
∵原点0是线段AB的中点,∴A(x1,y1) 与B(x2,y2)关于原点中心对称,∴x1=-x2,y1=-y2∵y=2x2+4x-2=2(x+1)2-4,∴抛物线的对称轴为直线x=-1,顶点坐标为(-1,-4),∴A点和B点在第一、三象限,设A点在第一象限,∴B点坐标为(- x1,-y1),∴y1=2x12+4x1-2,- y1=2x12-4x1-2∴x1=1,y1=4,∴A(1,4),B(-1,-4)∴AB=![]() =2
=2![]() ,故答案为2
,故答案为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

(1)根据图示填写下表:
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场代销甲、乙两种商品,其中甲种商品进价为120元/件,售价为130元/件,乙种商品进价为100元/件,售价为150元/件.
(1)若商场用36000元购进这两种商品若干,销售完后可获利润6000元,则该商场购进甲、乙两种商品各多少件?(列方程组解答)
(2)若商场购进这两种商品共100件,设购进甲种商品x件,两种商品销售后可获总利润为y元,请写出y与x的函数关系式(不要求写出自变量x的范围),并指出购进甲种商品件数x逐渐增加时,总利润y是增加还是减少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆
 中有折线
中有折线 ,
, ,
, ,
, ,则弦
,则弦 的长为_____.
的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,EG⊥BC于点G,连接AG、FG.下列结论:①AE=CE;②△ABF≌△GBF;③BE⊥AG;④△AEF为等腰三角形.其中正确结论的个数是( )
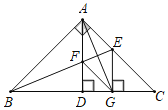
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
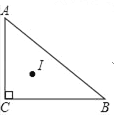
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片
 如图甲
如图甲 ,其中
,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙
如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙
如图丙 原三角形纸片ABC中,
原三角形纸片ABC中, 的大小为______
的大小为______

相关试题

