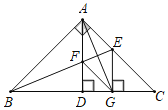
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,EG⊥BC于点G,连接AG、FG.下列结论:①AE=CE;②△ABF≌△GBF;③BE⊥AG;④△AEF为等腰三角形.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
利用全等三角形的性质以及角平分线的性质定理一一判断即可.
∵BF平分∠ABC,∠BAC=90°,EG⊥BC
∴AE=EG,
∵EC>EG,
∴EC>AE,故①错误,
∵AE=EG,BE=BE
∴Rt△ABE≌Rt△GBE(HL)
∴AB=BG,
∴点B在AG的垂直平分线上,
∵AE=EG
∴点E在AG的垂直平分线上
∴BE是AG的垂直平分线
∴BE⊥AG,故③正确,
∵BA=BG,∠ABF=∠GBF,BF=BF,
∴△ABF≌△GBF(SAS),故②正确,
∵BE是AG的垂直平分线
∴AF=FG,EF⊥AG
∴∠AFE=∠EFG
∵AD⊥BC,EG⊥BC
∴AD∥EG
∴∠AFE=∠FEG
∴∠EFG=∠FEG
∴FG=EG
∴AF=FG=EG=AE,故④正确,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场代销甲、乙两种商品,其中甲种商品进价为120元/件,售价为130元/件,乙种商品进价为100元/件,售价为150元/件.
(1)若商场用36000元购进这两种商品若干,销售完后可获利润6000元,则该商场购进甲、乙两种商品各多少件?(列方程组解答)
(2)若商场购进这两种商品共100件,设购进甲种商品x件,两种商品销售后可获总利润为y元,请写出y与x的函数关系式(不要求写出自变量x的范围),并指出购进甲种商品件数x逐渐增加时,总利润y是增加还是减少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆
 中有折线
中有折线 ,
, ,
, ,
, ,则弦
,则弦 的长为_____.
的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 、
、 是抛物线
是抛物线 上的点,坐标系原点
上的点,坐标系原点 位于线段
位于线段 的中点处,则
的中点处,则 的长为_____.
的长为_____. -
科目: 来源: 题型:
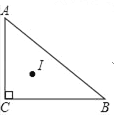
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片
 如图甲
如图甲 ,其中
,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙
如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙
如图丙 原三角形纸片ABC中,
原三角形纸片ABC中, 的大小为______
的大小为______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.

(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(3,1),在此坐标系下,B点的坐标为 ;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为 ;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c的图象过O、B、C三点,D为此抛物线的顶点。试求出抛物线解析式及D点的坐标。
相关试题

