【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0).有下列命题:①若a+b+c=0,则b2-4ac≥0;②若一元二次方程ax2+bx+c=0的两根为-1和2,则2a+c=0;③若一元二次方程ax2+c=0有两个不相等的实数根,则一元二次方程ax2+bx+c=0必有两个不相等的实数根.其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
参考答案:
【答案】D
【解析】试题解析:①若a+b+c=0,方程ax2+bx+c=0有一根为1,又a≠0,则b2-4ac≥0,正确;
②由两根关系可知,-1×2=![]() ,整理得:2a+c=0,正确;
,整理得:2a+c=0,正确;
③若方程ax2+c=0有两个不相等的实根,则-4ac>0,可知b2-4ac>0,故方程ax2+bx+c=0必有两个不相等的实根,正确.
正确命题有三个.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式 x3+(﹣k+1)2x2﹣3x+1 中不含 x2 项,则 k 的值为( )
A. 0 B. 1 C. ﹣1 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师布置了两道解方程的作业题:
(1)选用合适的方法解方程:(x+1)(x+2)=6;
(2)用配方法解方程:2x2+4x-5=0.
以下是小明同学的作业:
(1)解:由(x+1)(x+2)=6,
(2)解:由2x2+4x-5=0,
得x+1=2,x+2=3,
得2x2+4x=5,
所以x1=1,x2=1.
x2+2x=
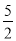 ,
,x2+2x+1=
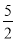 -1,
-1,(x+1)2=
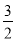 ,
,x+1=±
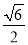
x1=-1+
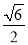 ,x2=-1-
,x2=-1-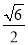 .
.请你帮小明检查他的作业是否正确,把不正确的改正过来.
-
科目: 来源: 题型:
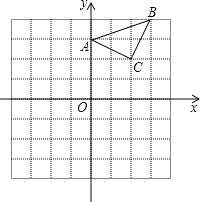
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A.k≤﹣4
B.k≥﹣4
C.k≤4
D.k>4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法: ①a>0;②c>0;③4a﹣b+c<0;④当﹣1<x<3时,y>0.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
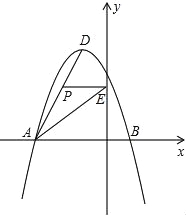
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
相关试题

