【题目】已知等边△ABC的边长为![]() ,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
设BD=x,根据等边三角形的性质得到∠A=∠B=∠C=60°,由垂直的定义得到∠BDF=∠DEA=∠EFC=90°,解直角三角形即可得到结论.
如图,设BD=x,
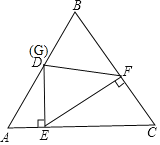
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE⊥AC于点E,EF⊥BC于点F,FG⊥AB,
∴∠BDF=∠DEA=∠EFC=90°,
∴∠ADE=∠CEF=∠BFD=30°,
∴BF=2BD=2x,
∴CF=18-2x,
∴CE=2CF=36-4x,
∴AE=18-CE=4x-18,
∴AD=2AE=8x-36,
∵AD+BD=AB,
∴8x-36+x=18,
∴x=6,
∴AD=8x-36=48-36=12,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:
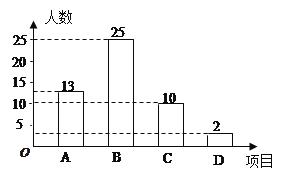
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;

(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】纪中三鑫双语学校准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).

根据以上统计图提供的信息,请解答下列问题:
(1)m= ,n= .
(2)补全上图中的条形统计图.
(3)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的
 ;
;(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
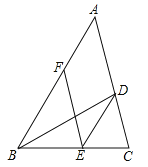
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线
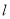 起跑,绕过
起跑,绕过 点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.
点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.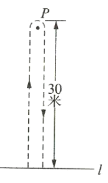
相关试题

