【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌![]() ,△AEB≌
,△AEB≌![]() ,且
,且![]() ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )

A.105°B.100°C.110°D.115°
参考答案:
【答案】B
【解析】
延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′+∠CAD,再求出∠C′+∠AHC′即可解决问题.
解:延长C′D交AB′于H.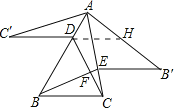
∵△AEB≌△AEB′,
∴∠ABE=∠B′,∠EAB=∠EAB′=40°,
∵C′H∥EB′,
∴∠AHC′=∠B′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,∠DAC=∠DAC′=40°,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠CAD,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=10,AC=
 ,BC 边上的高 AD=6,则另一边 BC 等于( )
,BC 边上的高 AD=6,则另一边 BC 等于( )A.10B.8C.6 或 10D.8 或 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 垂直平分线段
垂直平分线段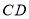 (
( ),点
),点 是线段
是线段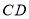 延长线上的一点,且
延长线上的一点,且 ,连接
,连接 ,过点
,过点 作
作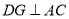 于点
于点 ,交
,交 的延长线与点
的延长线与点 .
.
(1)若
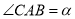 ,则
,则 ______(用
______(用 的代数式表示);
的代数式表示);(2)线段
 与线段
与线段 相等吗?为什么?
相等吗?为什么?(3)若
 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )

A.20°B.30°C.25°D.15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】操作发现:
 如图1,将直角三角板的直角顶点放在正方形ABCD上,使直角顶点E与正方形ABCD的顶点D重合,直角的一边交CB于点F,将另一边交BA的延长线于点
如图1,将直角三角板的直角顶点放在正方形ABCD上,使直角顶点E与正方形ABCD的顶点D重合,直角的一边交CB于点F,将另一边交BA的延长线于点 请你直接回答EF和EG的数量关系;
请你直接回答EF和EG的数量关系;类比探究
 如图2,当三角板的直角顶点E在正方形ABCD的对角线BD上运动时,其余条件不变,
如图2,当三角板的直角顶点E在正方形ABCD的对角线BD上运动时,其余条件不变, 中的结论还成立吗?并说明理由;
中的结论还成立吗?并说明理由;拓展延伸
 如图3,将“正方形ABCD”改成“矩形ABCD”,当直角顶点移动到图中所示位置时,若
如图3,将“正方形ABCD”改成“矩形ABCD”,当直角顶点移动到图中所示位置时,若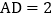 ,
, ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的解析式为
 ,抛物线
,抛物线 与y轴交于点A,与x轴交于点
与y轴交于点A,与x轴交于点 ,点P是抛物线上一动点,设点P的横坐标为m.
,点P是抛物线上一动点,设点P的横坐标为m. 求抛物线的解析式;
求抛物线的解析式; 如图
如图 ,当点P在第一象限内的抛物线上时,求
,当点P在第一象限内的抛物线上时,求 面积的最大值,并求此时点P的坐标;
面积的最大值,并求此时点P的坐标; 过点A作直线
过点A作直线 轴,过点P作
轴,过点P作 于点H,将
于点H,将 绕点A顺时针旋转,使点H的对应点
绕点A顺时针旋转,使点H的对应点 恰好落在直线AB上,同时
恰好落在直线AB上,同时 恰好落在坐标轴上,请直接写出点P的坐标.
恰好落在坐标轴上,请直接写出点P的坐标.
相关试题

