【题目】如图,![]() 垂直平分线段
垂直平分线段![]() (
(![]() ),点
),点![]() 是线段
是线段![]() 延长线上的一点,且
延长线上的一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线与点
的延长线与点![]() .
.

(1)若![]() ,则
,则![]() ______(用
______(用![]() 的代数式表示);
的代数式表示);
(2)线段![]() 与线段
与线段![]() 相等吗?为什么?
相等吗?为什么?
(3)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)45°-α;(2)相等,理由见解析;(3)3![]()
【解析】
(1)根据等腰三角形的性质得到∠BAE=∠AEB=45°,根据三角形的内角和即可得到结论;
(2)连接AD,根据线段垂直平分线的性质得到AC=AD,求得∠ADC=∠ACB=α,于是得到AC=DF;
(3)根据已知条件得到BD=CB=3,过F作FH⊥CE交CE的延长线于H,得到△EHF是等腰直角三角形,求得FH=HE,根据全等三角形的性质即可得到结论.
(1)∵AB⊥CD,
∴∠ABE=90°,
∵AB=BE,
∴∠BAE=∠AEB=45°,
∵∠CAB=α,∠CDG=90°-(90°-α)=α=∠EDF.
∴∠AFG=∠AED-∠EDF=45°-α;
故答案为:45°-α;
(2)相等,
证明:连接AD,
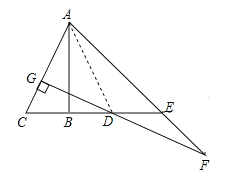
∵AB垂直平分线段CD,
∴AC=AD,
∴∠ADC=∠ACB=90°-α,
∴∠DAE=∠ADC-45°=45°-α,
∴∠DAE=∠AFD,
∴AD=DF,
∴AC=DF;
(3)∵CD=6,
∴BD=CB=3,
过F作FH⊥CE交CE的延长线于H,
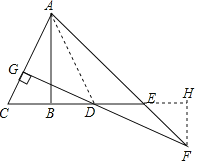
则△EHF是等腰直角三角形,
∴FH=HE,
∵∠H=∠ABC=90°,∠CAB=∠CDG=∠FDH,AC=AD=DF,
∴△ACB≌△DFH(AAS),
∴FH=CB=3,
∴EF=![]() FH=3
FH=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 的坐标分别为
的坐标分别为 ,将
,将 绕点
绕点 旋转
旋转 后得到
后得到 ,其中点
,其中点 的对应点
的对应点 的坐标为
的坐标为 .
.(1)求出点
 的坐标;
的坐标;(2)求点
 的坐标,并求出点
的坐标,并求出点 的对应点
的对应点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球
排球
进价(元/个)
80
50
售价(元/个)
95
60
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正比例函数的图象经过点
 ,则下列点也在该函数图象上的是( )
,则下列点也在该函数图象上的是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 张看上去无差别的卡片,上面分别写着
张看上去无差别的卡片,上面分别写着 ,随机抽取
,随机抽取 张后,放回并混在一起,再随机抽取
张后,放回并混在一起,再随机抽取 张.
张.(1)请用树状图或列表法等方法列出各种可能出现的结果;
(2)求两次抽到的卡片上的数字之和等于
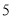 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.
(1)求出乙、丙两种书的每本各多少元?
(2)若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?
(3)在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?
(4)七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?
相关试题

