【题目】操作发现:
![]() 如图1,将直角三角板的直角顶点放在正方形ABCD上,使直角顶点E与正方形ABCD的顶点D重合,直角的一边交CB于点F,将另一边交BA的延长线于点
如图1,将直角三角板的直角顶点放在正方形ABCD上,使直角顶点E与正方形ABCD的顶点D重合,直角的一边交CB于点F,将另一边交BA的延长线于点![]() 请你直接回答EF和EG的数量关系;
请你直接回答EF和EG的数量关系;
类比探究
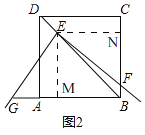
![]() 如图2,当三角板的直角顶点E在正方形ABCD的对角线BD上运动时,其余条件不变,
如图2,当三角板的直角顶点E在正方形ABCD的对角线BD上运动时,其余条件不变,![]() 中的结论还成立吗?并说明理由;
中的结论还成立吗?并说明理由;
拓展延伸
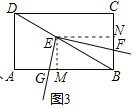
![]() 如图3,将“正方形ABCD”改成“矩形ABCD”,当直角顶点移动到图中所示位置时,若
如图3,将“正方形ABCD”改成“矩形ABCD”,当直角顶点移动到图中所示位置时,若![]() ,
,![]() ,求
,求![]() 的值.
的值.

参考答案:
【答案】(1)![]() ;(2)结论成立,理由见解析;(3)
;(2)结论成立,理由见解析;(3)![]() .
.
【解析】
(1)先判断出CDF=∠ADG,进而判断出△CDF≌△ADG,即可得出DF=DG结论得证;
(2)先构造出图形,判断出∠NEF=∠MEG,进而判断出△NEF≌△MEG,即可得出EF=EG;
(3)先判断出∠NEF=∠MEG,进而判断出△ENF∽△EMG,得出 ![]() ,再证明
,再证明![]() 即可解决问题;即可得出结论.
即可解决问题;即可得出结论.
![]() 证明:
证明:![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 点D和E重合,
点D和E重合,
![]() ;
;
![]() 解:结论成立.
解:结论成立.
理由:如图2,
过点E作![]() 于N,
于N,![]() 于M,
于M,
![]() 点E在正方形ABCD的对角线BD上,
点E在正方形ABCD的对角线BD上,
![]() 四边形EMBN是正方形,
四边形EMBN是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
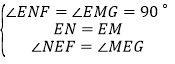 ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() 解:如图3,过点E作
解:如图3,过点E作![]() 于N,
于N,![]() 于M,
于M,
![]() 四边形EMBN是矩形,
四边形EMBN是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )

A.20°B.30°C.25°D.15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌
 ,△AEB≌
,△AEB≌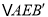 ,且
,且 ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105°B.100°C.110°D.115°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的解析式为
 ,抛物线
,抛物线 与y轴交于点A,与x轴交于点
与y轴交于点A,与x轴交于点 ,点P是抛物线上一动点,设点P的横坐标为m.
,点P是抛物线上一动点,设点P的横坐标为m. 求抛物线的解析式;
求抛物线的解析式; 如图
如图 ,当点P在第一象限内的抛物线上时,求
,当点P在第一象限内的抛物线上时,求 面积的最大值,并求此时点P的坐标;
面积的最大值,并求此时点P的坐标; 过点A作直线
过点A作直线 轴,过点P作
轴,过点P作 于点H,将
于点H,将 绕点A顺时针旋转,使点H的对应点
绕点A顺时针旋转,使点H的对应点 恰好落在直线AB上,同时
恰好落在直线AB上,同时 恰好落在坐标轴上,请直接写出点P的坐标.
恰好落在坐标轴上,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,则AB=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为____.

相关试题

