【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
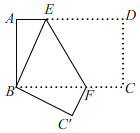
A.122.5°B.130°C.135°D.140°
参考答案:
【答案】A
【解析】
由折叠的性质知:∠EBC′、∠BC′F都是直角,因此BE∥C′F,那么∠EFC′和∠BEF互补,欲求∠EFC′的度数,需先求出∠BEF的度数;根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,由此可求出∠BEF的度数,即可得解.
解:Rt△ABE中,∠ABE=25°,
∴∠AEB=![]() 65°;
65°;
由折叠的性质知:∠BEF=∠DEF;
而∠BED=180°﹣∠AEB=115°,
∴∠BEF=![]() 57.5°;
57.5°;
∵∠EBC′=∠D=∠BC′F=∠C=90°,
∴BE∥C′F,
![]()
∴∠EFC′=180°﹣∠BEF=122.5°.
故选:A.
-
科目: 来源: 题型:
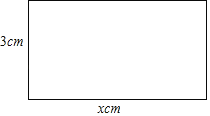
查看答案和解析>>【题目】如图,已知长方形相邻两边的长分别是xcm和3cm,设长方形的面积为ycm2.
(1)试写出长方形的面积y与x之间的关系式;
(2)利用(1)中的关系式,求当x=5cm时长方形的面积;
(3)当x的值由4cm变化到12cm时,长方形的面积由 cm2变化到 cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

-
科目: 来源: 题型:
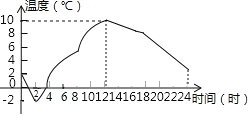
查看答案和解析>>【题目】如图是某地某一天的气温随时间的变化而变化的图象,请根据图象回答:
(1)这一天什么时候气温最低?最低气温是多少?什么时候气温最高?最高气温是多少?
(2)求这一天的最大温差是多少?
(3)请你描述一下这一天气温随时间的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
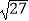 ﹣2cos30°+(
﹣2cos30°+(  )﹣2﹣|1﹣
)﹣2﹣|1﹣ 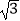 |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DEF是△ABC经过平移得到的.已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是( )

A. ∠F=90° B. ∠BED=∠FED C. BC⊥DF D. DF∥AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数
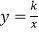 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )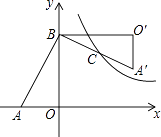
A.3
B.4
C.6
D.8
相关试题

