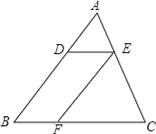
【题目】如图,在△ABC中,DE∥BC,EF∥AB,若S△ADE=4cm2,S△EFC=9cm2,求S△ABC.
参考答案:
【答案】25cm2.
【解析】试题分析:利用平行证明三角形相似,再利用相似的性质求三角形面积.
试题解析:
解:∵DE∥BC,EF∥AB,
∴∠A=∠FEC,∠AED=∠C,
∴△ADE∽△ECF;
∴S△ADE:S△ECF=(AE:EC)2,
∵S△ADE=4cm2,S△EFC=9cm2,
∴(AE:EC)2=4:9,
∴AE:EC=2:3,
即EC:AE=3:2,
∴(EC+AE):AE=5:2,
即AC:AE=5:2.
∵DE∥BC,
∴∠C=∠AED,
又∵∠A=∠A,
∴△ABC∽△ADE,
∴S△ABC:S△ADE=(AC:AE)2,
∴S△ABC:4=(5:2)2,
∴S△ABC=25cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了配合足球进校园的活动,实验学校在体育用品专卖店购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。求购买一个甲种足球,一个乙种足球各需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,-1)、B(2,0)、C(0,3),AC交
 轴于点D,AB交
轴于点D,AB交 轴于点E.
轴于点E.(1)△ABC的面积为________;
(2)点E的坐标为________;
(3)若点P的坐标为(0,
 ):
):①线段EP的长为________(用含
 的式子表示);
的式子表示);②当
 时,求点P的坐标。
时,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一
A:计时制:0.05元/分,B:包月制:50元/月,此外,每一种上网时间都要收通信费0.02元/分
(1)某用户某月上网时间为x小时,请写出两种收费方式下该用户应该支付的费用(用y表示)
(2)若甲用户估计一个月上网时间为20小时,乙用户估计一个月上网时间为15小时,各选哪一种收费方式最合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程
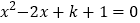 有两个不相等的实数根x1,x2.
有两个不相等的实数根x1,x2. (1)求k的取值范围;
(2)如果
 ,且k为整数,求k的值.
,且k为整数,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

相关试题

