【题目】在平面直角坐标系中,已知点A(O,1),B(1,2),点P在![]() 轴上运动,当点P到A、B两点的距离之差的绝对值最大时,该点记为点P1,当点P到A、B两点的距离之和最小时,该点记为点P2,以P1P2为边长的正方形的面积为
轴上运动,当点P到A、B两点的距离之差的绝对值最大时,该点记为点P1,当点P到A、B两点的距离之和最小时,该点记为点P2,以P1P2为边长的正方形的面积为
A. 1 B. ![]() C.
C. ![]() D. 5
D. 5
参考答案:
【答案】C
【解析】
由三角形两边之差小于第三边可知,当A、B、P三点不共线时,|PA-PB|<AB,又因为A(0,1),B(1,2)两点都在x轴同侧,则当A、B、P三点共线时,|PA-PB|=AB,即|PA-PB|≤AB,所以当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.先运用待定系数法求出直线AB的解析式,再令y=0,求出x的值即可得到点P1的坐标;点A关于x轴的对称点为A',求得直线A'B的解析式,令y=0,即可得到点P2的坐标,进而得到以P1P2为边长的正方形的面积.
由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
设直线AB的解析式为y=kx+b,
∵A(0,1),B(1,2),
∴![]() ,解得
,解得![]() ,
,
∴y=x+1,
令y=0,则0=x+1,
解得x=-1.
∴点P1的坐标是(-1,0).
∵点A关于x轴的对称点A'的坐标为(0,-1),
设直线A'B的解析式为y=k'x+b',
∵A'(0,-1),B(1,2),
![]() ,解得
,解得![]() ,
,
∴y=3x1,
令y=0,则0=3x1,
解得x=![]() ,
,
∴点P2的坐标是(![]() ,0).
,0).
∴以P1P2为边长的正方形的面积为(![]() +1)2=
+1)2=![]() ,
,
-
科目: 来源: 题型:
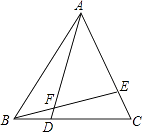
查看答案和解析>>【题目】如图,△ABC是等边三角形,D、E分别是BC、AC上的点,BD=CE,求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 的长.
的长. -
科目: 来源: 题型:
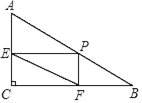
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE= °
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).

相关试题

