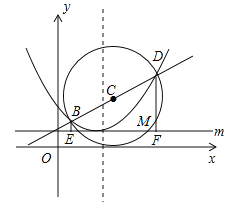
【题目】如图,已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
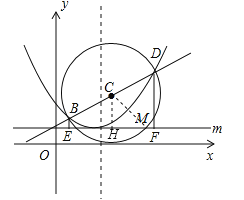
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线![]() 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)可设抛物线的顶点式,再结合抛物线过点(4,2),可求得抛物线的解析式;
(2)联立直线和抛物线解析式可求得B、D两点的坐标,则可求得C点坐标和线段BD的长,可求得圆的半径,可证得结论;
(3)过点C作CH⊥m于点H,连接CM,可求得MH,利用(2)中所求B、D的坐标可求得FH,则可求得MF和BE的长,可求得其比值.
试题解析:
(1)∵已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为
(a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为![]() ,∵抛物线经过点(4,2),∴
,∵抛物线经过点(4,2),∴![]() ,解得a=
,解得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,即
,即![]() ;
;
(2)联立直线和抛物线解析式可得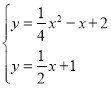 ,解得:
,解得: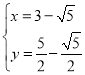 或
或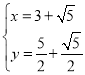 ,∴B(
,∴B(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∵C为BD的中点,∴点C的纵坐标为
),∵C为BD的中点,∴点C的纵坐标为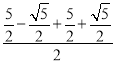 =
=![]() ,∵BD=
,∵BD=![]() =5,∴圆的半径为
=5,∴圆的半径为![]() ,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
(3)如图,过点C作CH⊥m,垂足为H,连接CM,由(2)可知CM=![]() ,CH=
,CH=![]() ﹣1=
﹣1=![]() ,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=
,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=![]() =
=![]() ,∴MF=HF﹣MH=
,∴MF=HF﹣MH=![]() ,∵BE=
,∵BE=![]() ﹣1=
﹣1=![]() ,∴
,∴![]() =
=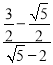 =
=![]() .
.
-
科目: 来源: 题型:
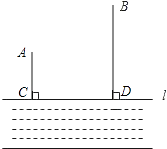
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P(x,y)在第三象限,且到y 轴距离为3,到x 轴距离为5,则P点的坐标是( )
A. (-3,-5) B. (5,-3) C. (3,-5) D. (-3,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为40°,则它的顶角的度数为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x+8与﹣2x﹣10的值互为相反数,则x的值为_____.
-
科目: 来源: 题型:
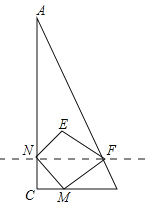
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
相关试题

