【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?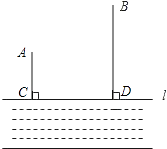
参考答案:
【答案】解:作A关于CD的对称点A′,连接A′B与CD,交点CD于M,点M即为所求作的点,
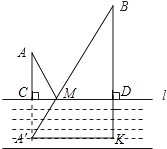
则可得:DK=A′C=AC=10千米,
∴BK=BD+DK=40千米,
∴AM+BM=A′B= ![]() =50千米,
=50千米,
总费用为50×3=150万元.
【解析】根据题意作出对称点,得到使铺设水管的费用最节省,再根据勾股定理求出总费用.
【考点精析】掌握轴对称-最短路线问题是解答本题的根本,需要知道已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣xa+2y3与6x5yb﹣2是同类项,则ab的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6
B.12
C.16
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个比3大且比4小的无理数: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P(x,y)在第三象限,且到y 轴距离为3,到x 轴距离为5,则P点的坐标是( )
A. (-3,-5) B. (5,-3) C. (3,-5) D. (-3,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
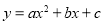 (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
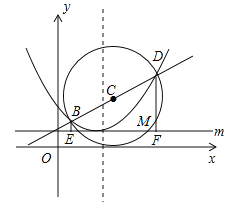
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线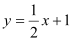 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
相关试题

